Display Title
Definition--Functions and Relations Concepts--Continuous Function
Display Title
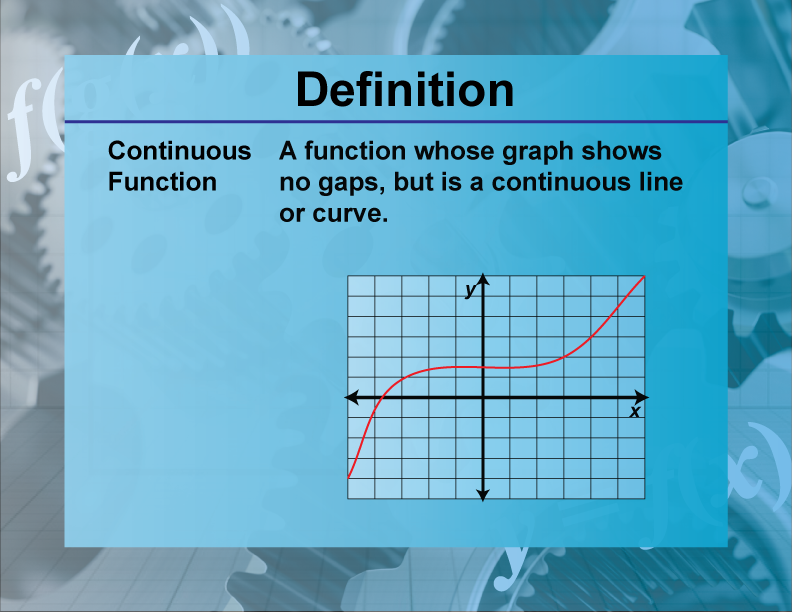
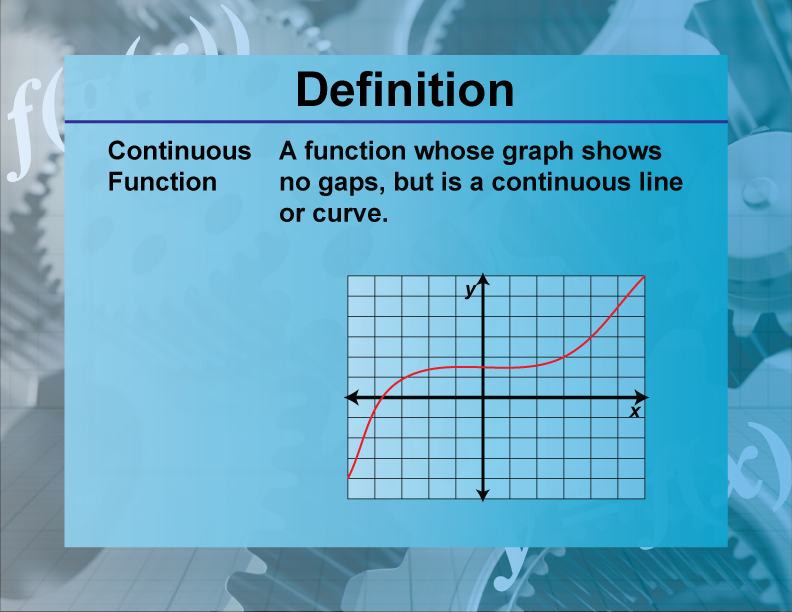
Continuous Function
Topic
Functions and Relations
Definition
A continuous function is a function that does not have any breaks, holes, or gaps in its domain.
Description
Continuous functions are fundamental in calculus and mathematical analysis because they allow for the application of limits, derivatives, and integrals. A function f(x) is continuous if, for every point 𝑐 c in its domain,
lim x→c f(x) = f(c)
Continuous functions are used in various real-world applications, such as modeling natural phenomena like temperature changes, where values change smoothly over time. For example, the function f(x)=x2 is continuous because it has no breaks or gaps. Understanding continuous functions is crucial for studying advanced mathematical concepts and for applying mathematical models to real-world scenarios.
For a complete collection of terms related to functions and relations click on this link: Functions and Relations Collection
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.1, CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.B.3, CCSS.MATH.CONTENT.HSF.BF.B.4 |
|---|---|
| Grade Range | 6 - 9 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2021 |
| Keywords | definition, function, relations, glossary terms |