Display Title
Definition--Functions and Relations Concepts--Odd Function
Display Title
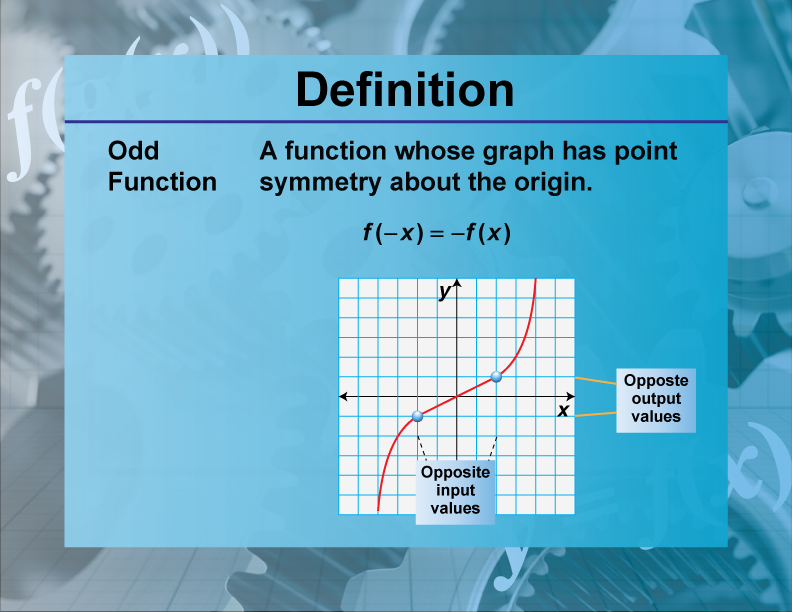
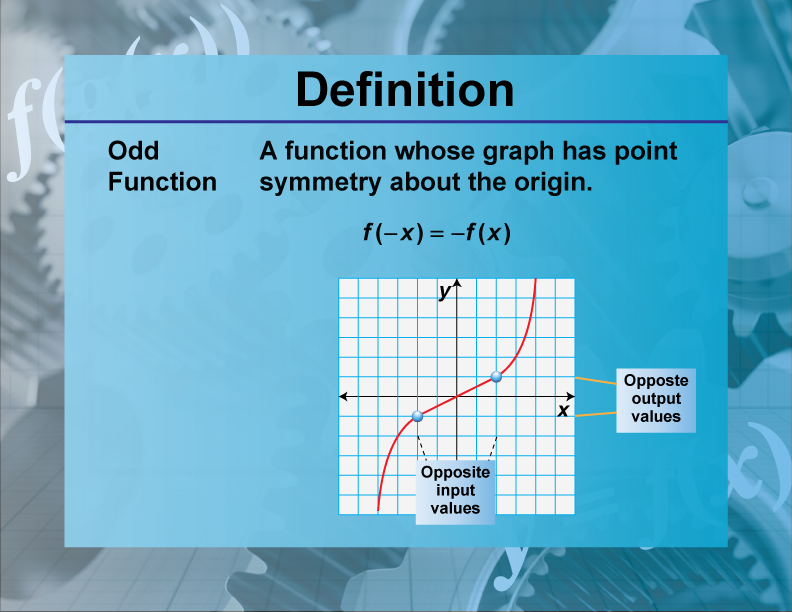
Odd Function
Topic
Functions and Relations
Definition
An odd function is a function that satisfies the condition f(−x) = −f(x) for all x in its domain.
Description
Odd functions are important in mathematics because they exhibit symmetry about the origin. This property is useful in various fields, including physics and engineering, where symmetry simplifies analysis and problem-solving. For example, the function f(x)=x3 is odd because f(−x) = −f(x). Odd functions are used to model phenomena that are symmetric with respect to the origin, such as alternating current in electrical engineering. Understanding odd functions helps in recognizing patterns and simplifying calculations in mathematical and real-world contexts.
For a complete collection of terms related to functions and relations click on this link: Functions and Relations Collection
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.1, CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.B.3, CCSS.MATH.CONTENT.HSF.BF.B.4 |
|---|---|
| Grade Range | 6 - 9 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2021 |
| Keywords | definition, function, relations, glossary terms |