Display Title
Definition--Geometry Basics--Incenter of a Triangle
Display Title
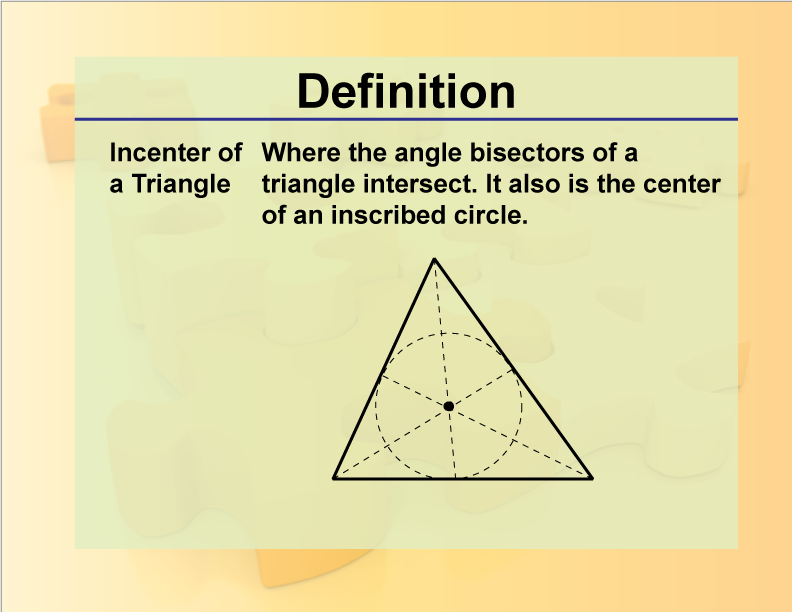
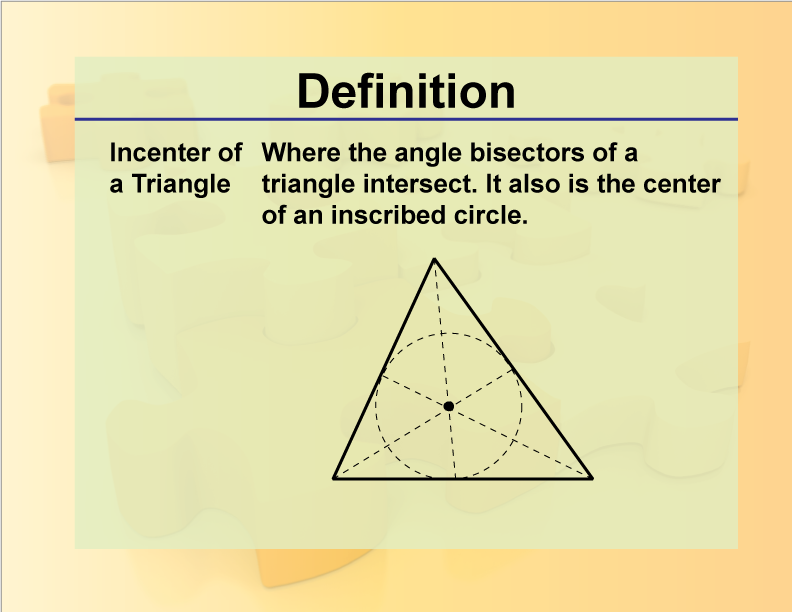
Incenter of a Triangle
Topic
Geometry Basics
Definition
The point where the angle bisectors of a triangle intersect.
Description
In geometry, the incenter of a triangle is crucial as it marks the center of the inscribed circle (incircle). This point has equal distances to all sides of the triangle, allowing it to touch each side precisely. Understanding the incenter is vital for calculations involving circle properties, such as area and radius in relation to triangle dimensions. The inradius can be determined using the triangle’s area and semi-perimeter. Comprehending this concept enhances problem-solving skills and mathematical understanding related to triangles and circles in geometry.
For a complete collection of terms related to Geometry Basics click on this link: Geometry Basics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSG.C.A.2, CCSS.MATH.CONTENT.HSG.C.A.1, CCSS.MATH.CONTENT.HSG.C.A.3, CCSS.MATH.CONTENT.HSG.C.A.4 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Geometry • Circles • Definition of a Circle |
| Copyright Year | 2020 |
| Keywords | trig ratios, trig identities |