Display Title
Definition--Linear Function Concepts--Decreasing Linear Function
Display Title
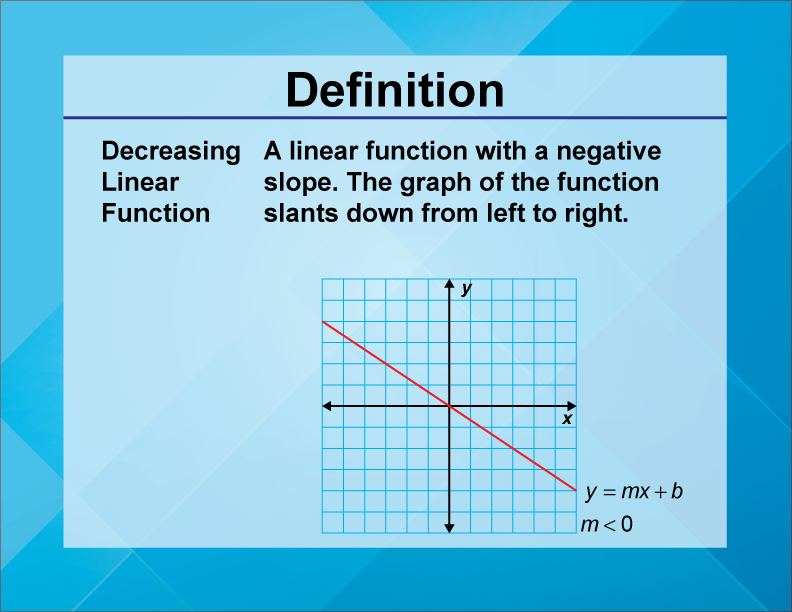
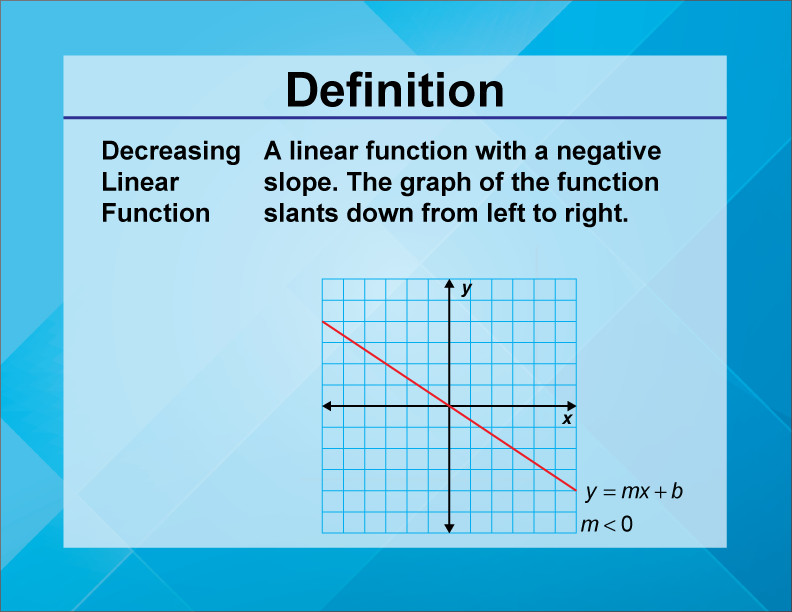
Decreasing Linear Function
Topic
Linear Functions
Definition
A decreasing linear function is a linear function where the slope is negative, indicating that as the input value increases, the output value decreases.
Description
Decreasing linear functions are important in understanding how variables inversely relate to each other. The negative slope signifies a reduction in the dependent variable as the independent variable increases.
Real-world examples include depreciation of assets over time or the decrease in temperature as altitude increases. These functions help model scenarios where an increase in one quantity results in a decrease in another.
In math education, recognizing and interpreting decreasing linear functions is essential for students. It aids in understanding negative slopes and their implications in various contexts, enhancing problem-solving skills and analytical thinking.
For a complete collection of terms related to linear functions and equations click on this link: Linear Functions and Equations Collection
| Common Core Standards | CCSS.MATH.CONTENT.8.SP.A.1, CCSS.MATH.CONTENT.HSA.SSE.A.1.A |
|---|---|
| Grade Range | 6 - 9 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope-Intercept Form |
| Copyright Year | 2021 |
| Keywords | linear functions, definitions, glossary term |