Definition--Measures of Central Tendency--Lower Quartile
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Probability and Data Analysis >> Data Analysis

Definition--Measures of Central Tendency--Lower Quartile

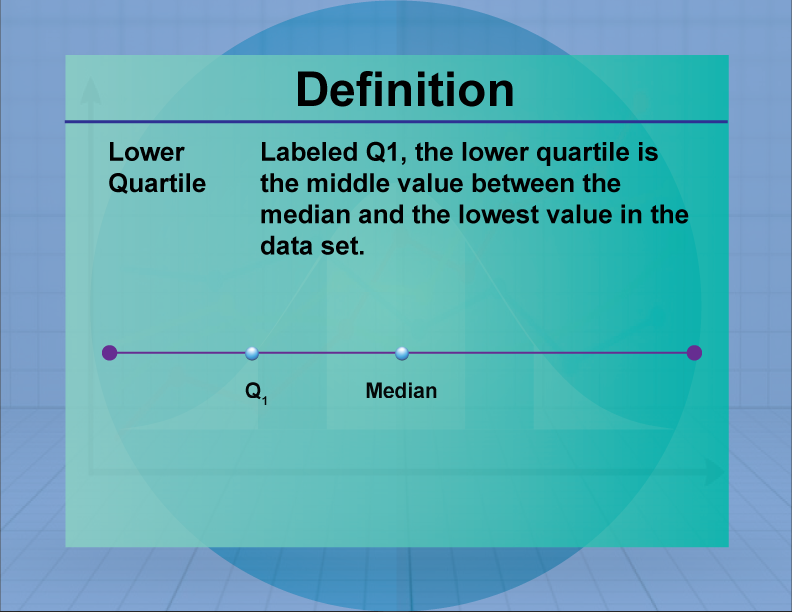
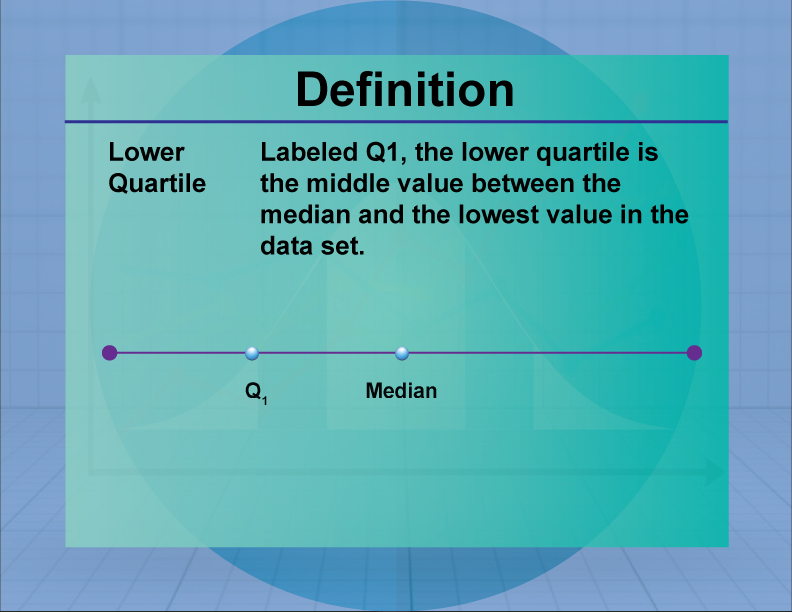
Lower Quartile

Lower Quartile

Topic

Statistics

Definition

The lower quartile (Q1) is the median of the lower half of a data set, representing the 25th percentile.

Description

The lower quartile is a measure of position, indicating the value below which 25% of the data falls. It is used in conjunction with other quartiles to understand the distribution and spread of data. In real-world applications, the lower quartile is used in finance to assess the performance of investments and in education to evaluate student achievement levels.

In math education, the lower quartile is introduced as part of lessons on data analysis and quartiles. Students learn to calculate and interpret the lower quartile using data sets and box plots, gaining insights into data distribution and variability. Teachers use the lower quartile to explain concepts of data position and its implications for decision-making, emphasizing its role in statistical analysis.

Lower Quartile
How can you tell if a child is in the lower quartile for height?

For a complete collection of terms related to Measures of Central Tendency click on this link: Measures of Central Tendency Collection.

Common Core Standards CCSS.MATH.CONTENT.HSS.CP.B.6, CCSS.MATH.CONTENT.HSS.CP.B.7, CCSS.MATH.CONTENT.HSS.CP.B.8, CCSS.MATH.CONTENT.HSS.CP.B.9, CCSS.MATH.CONTENT.HSS.MD.A.2, CCSS.MATH.CONTENT.HSS.MD.B.5, CCSS.MATH.CONTENT.HSS.MD.B.5.B, CCSS.MATH.CONTENT.HSS.MD.B.6, CCSS.MATH.CONTENT.HSS.MD.B.7
Grade Range 6 - 10
Curriculum Nodes Algebra
    • Probability and Data Analysis
        • Data Analysis
Copyright Year 2021
Keywords data analysis, measures of central tendency, definitions, glossary term, statistics, quartile