Display Title
Definition--Polygon Concepts--Geometric Constructions of Polygons
Display Title
Geometric Construction of a Polygon

Topic
Polygon Concepts
Definition
A polygon is a closed two-dimensional figure composed of straight line segments connected end to end.
Description
Polygons are fundamental shapes in geometry that play a crucial role in understanding various mathematical concepts and real-world applications. The geometric construction of a polygon involves creating a closed figure with a specific number of sides using precise mathematical methods. This process is essential for developing spatial reasoning skills and forms the basis for more complex geometric constructions. In geometry, polygons are classified based on their number of sides, regularity, and convexity. They range from simple triangles (3 sides) to complex figures with numerous sides.
The study of polygons encompasses important properties such as interior and exterior angles, diagonals, and symmetry. These properties are not only mathematically significant but also find practical applications in fields like architecture, computer graphics, and engineering. Understanding polygon construction and properties is crucial for solving various geometric problems, including area and perimeter calculations, tessellations, and the analysis of more complex shapes. Polygons also serve as building blocks for three-dimensional figures, making them indispensable in the study of solid geometry. Their relevance extends beyond pure mathematics, as polygons are frequently observed in nature, art, and design, highlighting the interconnectedness of geometry with the world around us.
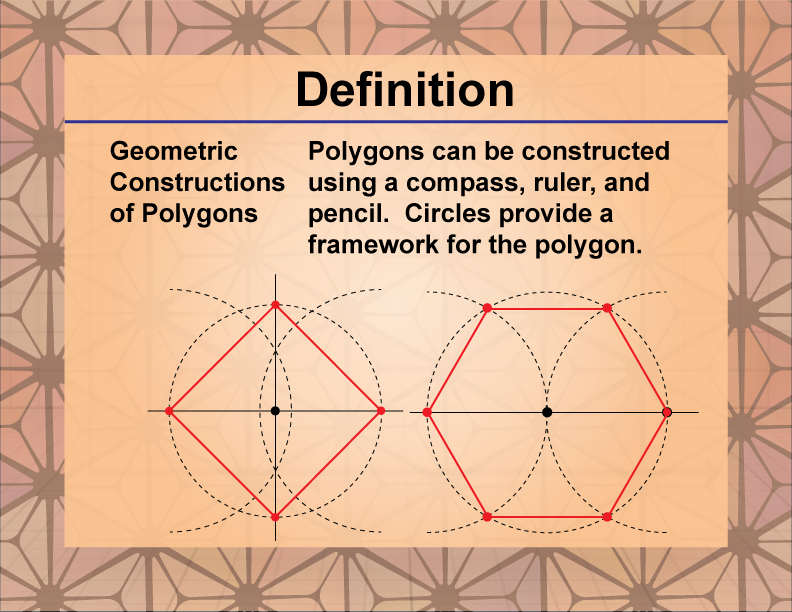
How to Create a Regular Hexagon
To create a regular hexagon using a compass, ruler, and pencil, follow these steps:
- Draw a circle using the compass. This circle will circumscribe the hexagon.
- Without changing the compass width, place the compass point on the circle's circumference and draw an arc that intersects the circle at two points.
- Repeat this process, placing the compass point at one of the intersection points created in step 2, and draw another arc to create two more intersection points.
- Continue this process until you have six equally spaced points around the circle's circumference.
- Using the ruler, connect these six points with straight lines to form the hexagon.
This method works because the radius of the circle is equal to the side length of the inscribed regular hexagon. The process effectively divides the circle into six equal 60° angles, creating a perfect regular hexagon.
Here's why this construction works:
- The radius of the circle becomes the side length of the hexagon.
- Each arc drawn from the circumference creates an equilateral triangle with two radii of the circle.
- The central angle of each of these triangles is 60°, which is exactly 1/6 of the full 360° of the circle.
This method is efficient and precise, requiring only a few simple steps to create a perfectly regular hexagon. It's widely used in geometric constructions and technical drawing.
For those without a compass, alternative methods exist, such as using a ruler to draw a horizontal line and then constructing 60° angles to form the hexagon's sides. However, the compass method described above is generally considered the most accurate and straightforward approach for creating a regular hexagon.
For a complete collection of terms related to polygons click on this link: Polygons Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.G.B.3, CCSS.MATH.CONTENT.5.G.B.4, CCSS.MATH.CONTENT.3.G.A.1, CCSS.MATH.CONTENT.3.MD.D.8, CCSS.MATH.CONTENT.6.G.A.1, CCSS.MATH.CONTENT.6.G.A.3, CCSS.MATH.CONTENT.HSG.CO.A.3 |
|---|---|
| Grade Range | 3 - 8 |
| Curriculum Nodes |
Geometry • Polygons • Definition of a Polygon |
| Copyright Year | 2021 |
| Keywords | polygon, definitions, glossary term |