Display Title
Definition--Polygon Concepts--Incenter
Display Title
Incenter of a Triangle

Topic
Polygons
Definition
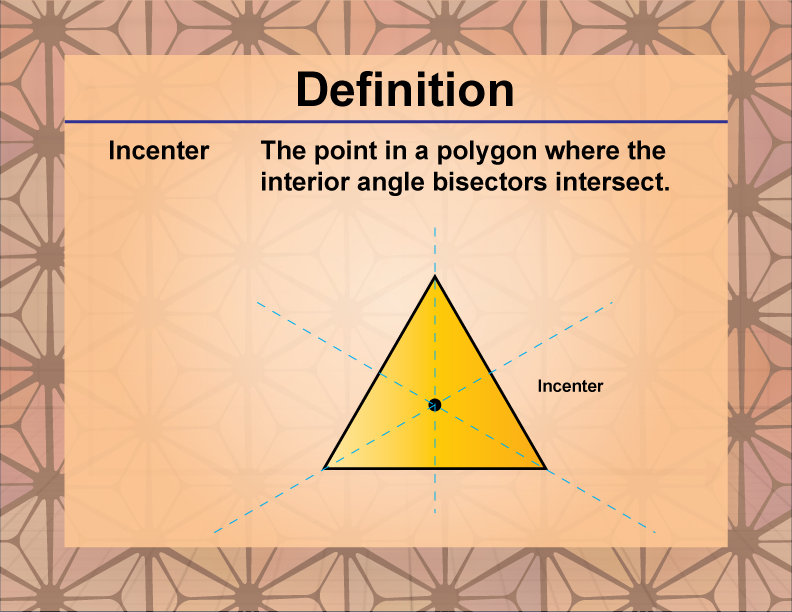
The incenter of a triangle is the point where the angle bisectors of the triangle intersect.
Description
The incenter is a significant point of concurrency in triangle geometry, offering valuable insights into the triangle's properties and symmetry. It is equidistant from all three sides of the triangle, making it the center of the largest circle that can be inscribed within the triangle (known as the incircle). This unique characteristic stems from the fact that angle bisectors are the loci of points equidistant from the sides of an angle. The incenter's position is influenced by the triangle's shape, always lying inside the triangle regardless of its type (acute, right, or obtuse).
In an equilateral triangle, the incenter coincides with other notable points such as the centroid, circumcenter, and orthocenter due to the triangle's perfect symmetry. For isosceles triangles, the incenter falls on the axis of symmetry. Understanding the incenter is crucial in various geometric constructions and proofs. It plays a role in solving problems related to inscribed circles, angle bisectors, and triangle congruence. The concept of the incenter extends beyond basic geometry, finding applications in advanced mathematics, engineering, and even architectural design where symmetry and balanced distribution of forces are essential.
For a complete collection of terms related to polygons click on this link: Polygons Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.G.B.3, CCSS.MATH.CONTENT.5.G.B.4, CCSS.MATH.CONTENT.3.G.A.1, CCSS.MATH.CONTENT.3.MD.D.8, CCSS.MATH.CONTENT.6.G.A.1, CCSS.MATH.CONTENT.6.G.A.3, CCSS.MATH.CONTENT.HSG.CO.A.3 |
|---|---|
| Grade Range | 3 - 8 |
| Curriculum Nodes |
Geometry • Polygons • Definition of a Polygon |
| Copyright Year | 2021 |
| Keywords | polygon, definitions, glossary term |