Display Title
Definition--Polygon Concepts--Inscribed Hexagon
Display Title
Inscribed Hexagon

Topic
Polygons and Circle Geometry
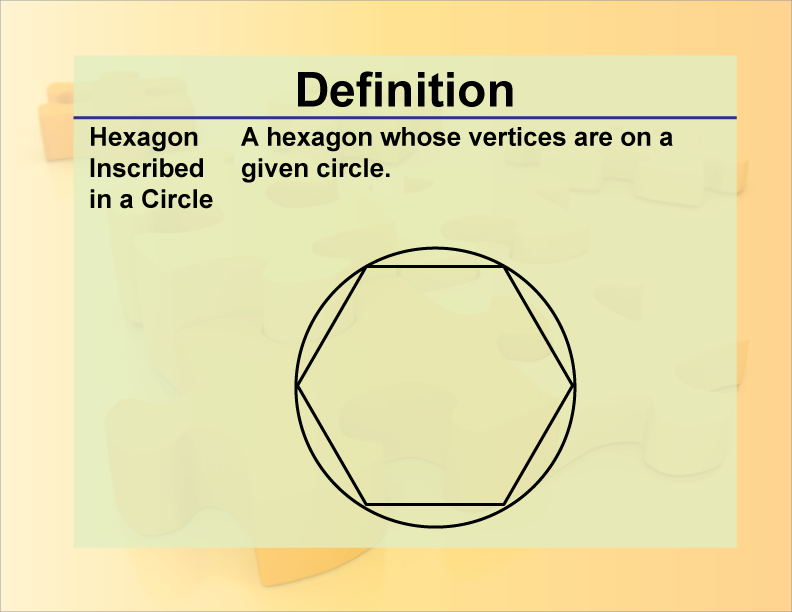
Definition
An inscribed hexagon is a six-sided polygon whose vertices all lie on the circumference of a circle.
Description
The inscribed hexagon is a fascinating geometric figure that exemplifies the intricate relationship between polygons and circles. In geometry, this shape is formed when all six vertices of a hexagon touch the circumference of a circle, creating a perfect fit within the circular boundary. This configuration has several interesting properties that make it significant in both theoretical and practical applications of mathematics. One of the most notable features of an inscribed hexagon is its symmetry. When properly constructed, it divides the circle into six equal arcs, each spanning 60 degrees. This property makes the inscribed hexagon an excellent tool for demonstrating concepts of rotational and reflective symmetry. Additionally, the radii drawn from the center of the circle to each vertex of the hexagon form six equilateral triangles, highlighting the deep connection between different geometric shapes.
In practical applications, inscribed hexagons are used in various fields, including architecture, engineering, and design. They provide a strong and efficient structure, which is why they're often seen in building designs and mechanical components. The study of inscribed hexagons also serves as a stepping stone to understanding more complex geometric concepts, such as the properties of other inscribed polygons and the relationships between regular polygons and circles.
For a complete collection of terms related to polygons click on this link: Polygons Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.G.B.3, CCSS.MATH.CONTENT.5.G.B.4, CCSS.MATH.CONTENT.3.G.A.1, CCSS.MATH.CONTENT.3.MD.D.8, CCSS.MATH.CONTENT.6.G.A.1, CCSS.MATH.CONTENT.6.G.A.3, CCSS.MATH.CONTENT.HSG.CO.A.3 |
|---|---|
| Grade Range | 3 - 8 |
| Curriculum Nodes |
Geometry • Polygons • Definition of a Polygon |
| Copyright Year | 2020 |
| Keywords | polygon, definitions, glossary term |