Display Title
Definition--Polynomial Concepts--Pascal's Triangle
Display Title
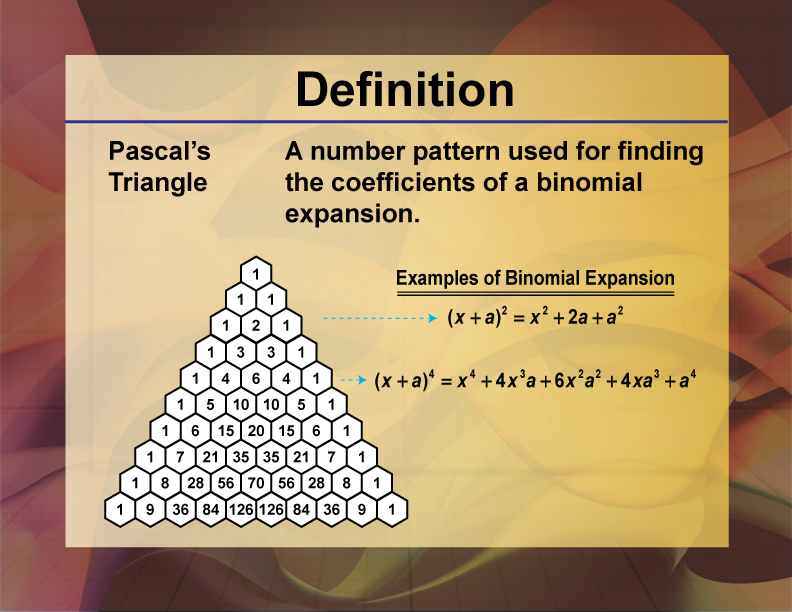
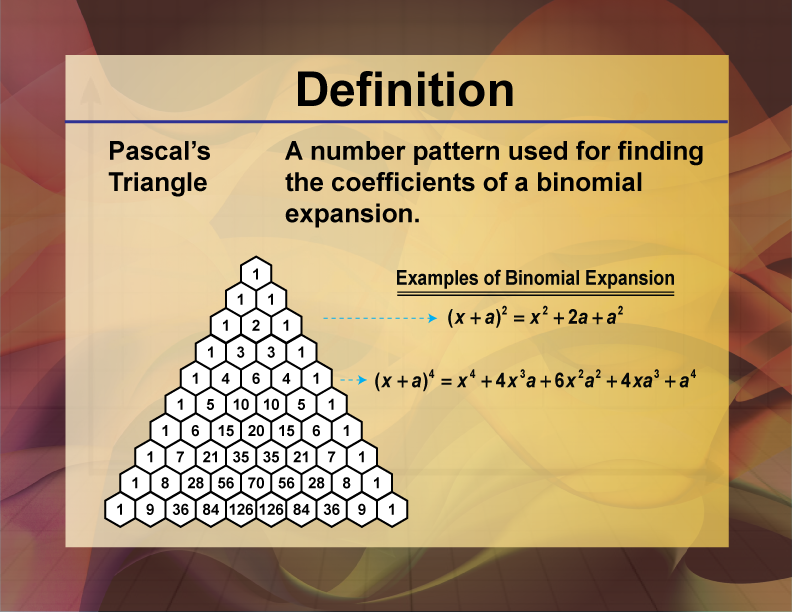
Pascal's Triangle
Topic
Polynomials
Definition
Pascal's Triangle is a triangular array of numbers where each number is the sum of the two directly above it.
Description
Pascal's Triangle is a mathematical structure that provides a wealth of information about binomial coefficients, polynomial expansions, and combinatorial relationships. Each row in Pascal's Triangle represents the coefficients of the expanded form of a binomial raised to a power, making it a valuable tool in algebra and combinatorics.
Understanding Pascal's Triangle is crucial for solving problems involving binomial expansions, combinations, and probability. It provides a visual and systematic way to determine the coefficients in polynomial expansions and to understand the relationships between different terms.
In practical applications, Pascal's Triangle is used in fields such as computer science, physics, and engineering to model and analyze complex systems. It helps in understanding the dynamics of algorithms, predicting outcomes, and solving problems involving combinatorial relationships. Mastery of Pascal's Triangle enhances problem-solving skills and provides a deeper understanding of polynomial and combinatorial concepts.
For a complete collection of terms related to polynomials click on this link: Polynomials Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSA.APR.A.1, CCSS.MATH.CONTENT.HSA.APR.B.2, CCSS.MATH.CONTENT.HSA.APR.C.5, CCSS.MATH.CONTENT.HSA.APR.C.4, CCSS.MATH.CONTENT.HSA.APR.B.3, CCSS.MATH.CONTENT.HSF.IF.C.7.C |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Expressions |
| Copyright Year | 2021 |
| Keywords | polynomials, monomials, definitions, glossary term, Pascal's Triangle |