Display Title
Definition--Polynomial Concepts--Volume Models with Polynomials
Display Title
Volume Models with Polynomials
Topic
Polynomials
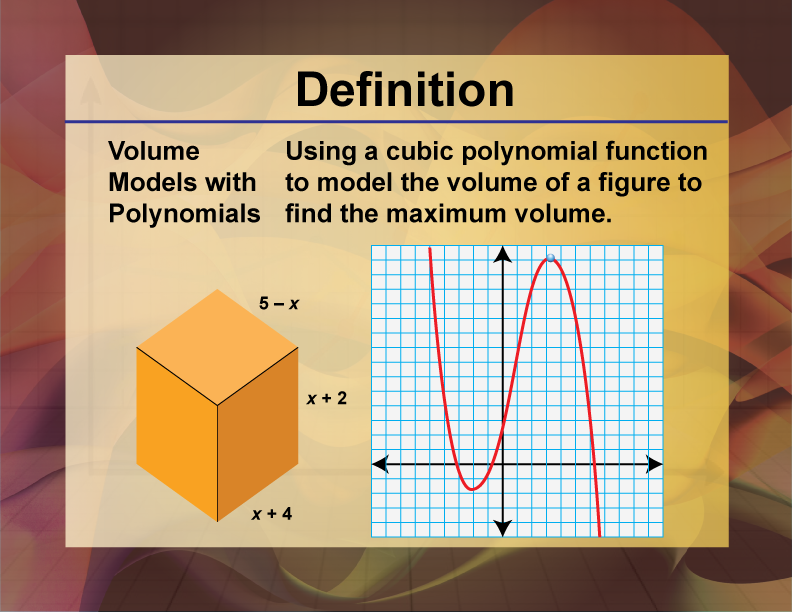
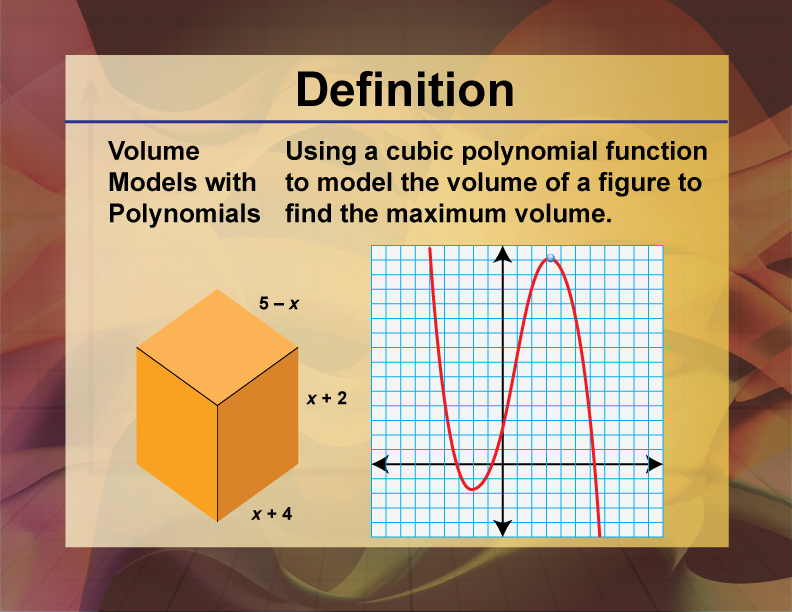
Definition
Volume models with polynomials involve using polynomial expressions to represent the volume of three-dimensional geometric shapes.
Description
Polynomials play a significant role in various fields of mathematics and applied sciences. In the context of volume models, polynomials are used to represent the dimensions and volume of geometric shapes. For instance, the volume of a rectangular prism can be expressed as a polynomial where the length, width, and height are variables. This allows for a flexible and powerful way to model and solve real-world problems involving three-dimensional spaces.
Volume models with polynomials are particularly useful in engineering, physics, and computer graphics, where precise calculations of volume are crucial. By expressing volumes as polynomials, it becomes easier to manipulate and compute these values, especially when dealing with complex shapes or when integrating over a region. Additionally, polynomial functions are foundational in calculus, where they are used to find volumes of solids of revolution and other complex structures through techniques such as integration.
Understanding how to construct and manipulate polynomial expressions is essential for students and professionals working in STEM fields. It provides a robust mathematical framework for tackling a wide range of problems, from simple geometric calculations to more advanced applications in science and technology.
For a complete collection of terms related to polynomials click on this link: Polynomials Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSA.APR.A.1, CCSS.MATH.CONTENT.HSA.APR.B.2, CCSS.MATH.CONTENT.HSA.APR.C.5, CCSS.MATH.CONTENT.HSA.APR.C.4, CCSS.MATH.CONTENT.HSA.APR.B.3, CCSS.MATH.CONTENT.HSF.IF.C.7.C |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Polynomials • Polynomial Expressions |
| Copyright Year | 2021 |
| Keywords | polynomials, monomials, definitions, glossary term |