Display Title
Definition--Quadratics Concepts--Axis of Symmetry
Display Title
Axis of Symmetry
Topic
Quadratics Concepts
Definition
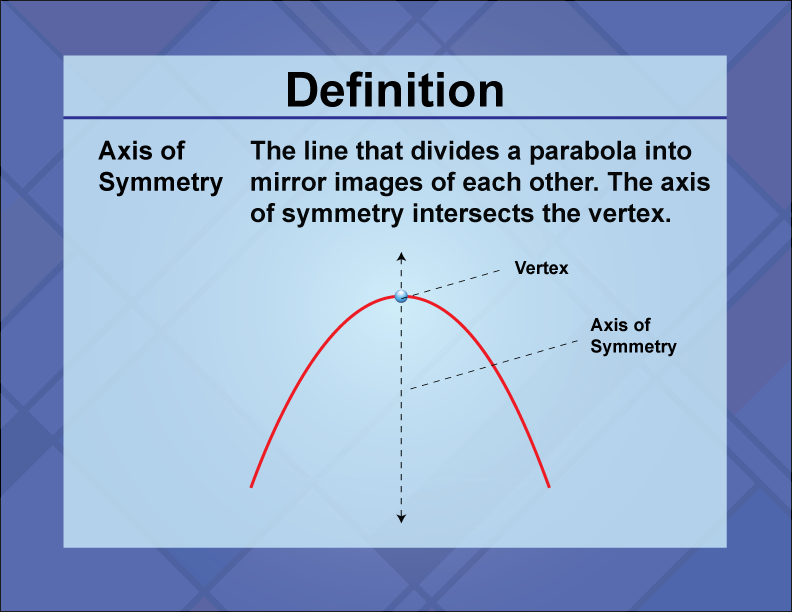
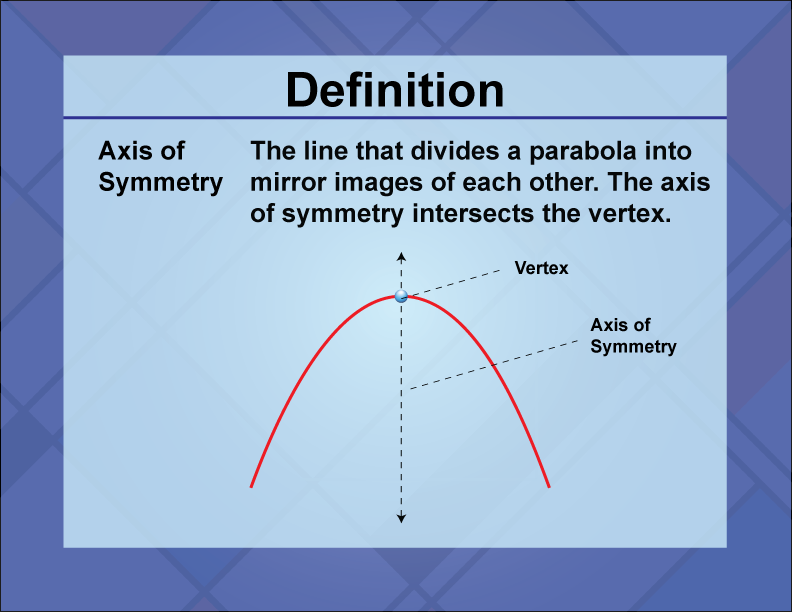
The axis of symmetry is a vertical line that divides a parabola into two mirror-image halves.
Description
The axis of symmetry is a fundamental concept in the study of quadratic functions and is crucial for understanding the geometric properties of parabolas. It is defined by the equation
x = −b/(2a)
for a quadratic equation in standard form
ax2 + bx + c = 0
This line passes through the vertex of the parabola, ensuring that each side of the parabola is a mirror image of the other. In real-world applications, the axis of symmetry is used in physics to analyze projectile motion, where the path of a projectile is parabolic. Understanding this concept helps in predicting the trajectory and determining the maximum height or range of the projectile. In math education, the axis of symmetry is vital for graphing quadratic functions, solving quadratic equations, and understanding the properties of parabolas. It provides a visual and algebraic method to explore the symmetry inherent in quadratic functions, enhancing students' comprehension of function behavior and graph analysis. An example of the axis of symmetry can be seen in the graph of the function
f(x) = x2 − 4x + 3
where the axis of symmetry is x = 2.
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms, axis of symmetry |