Display Title
Definition--Quadratics Concepts--Discriminant Visualization
Display Title
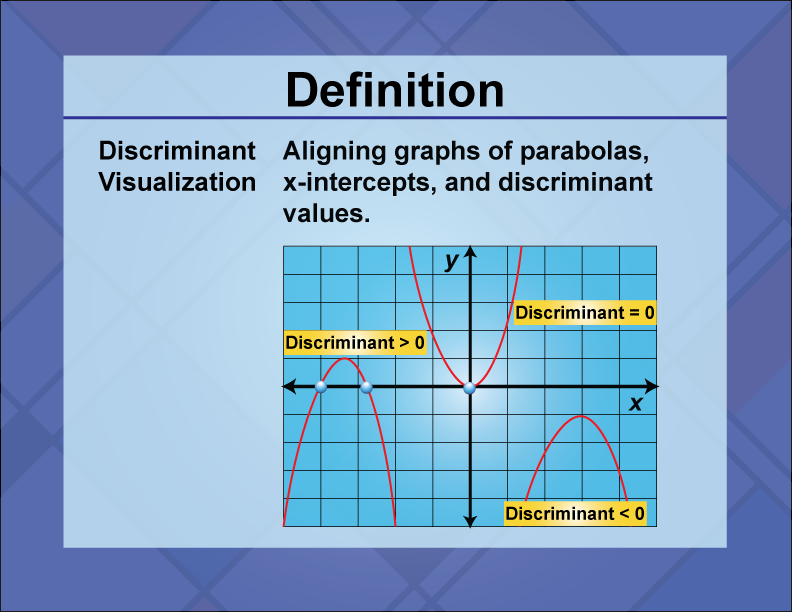
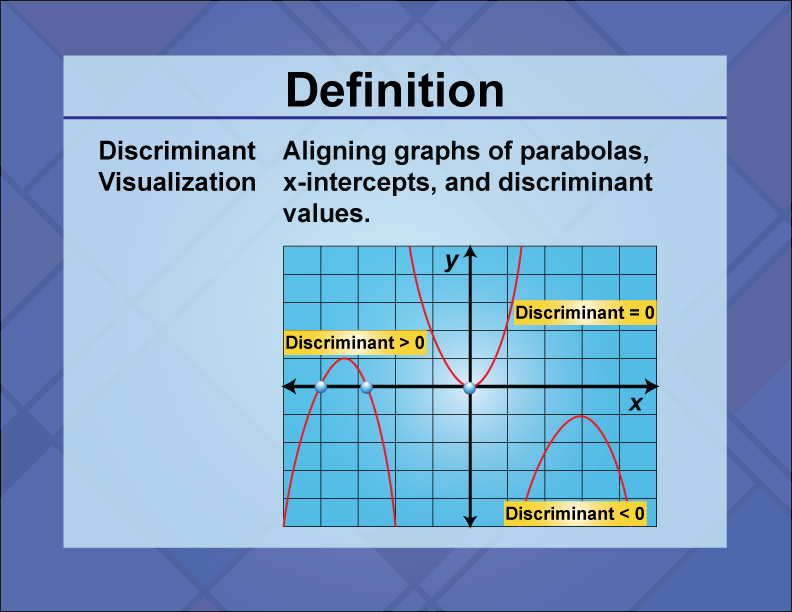
Discriminant Visualization
Topic
Quadratics Concepts
Definition
The discriminant is a value derived from a quadratic equation that indicates the nature of its roots.
Description
The discriminant of a quadratic equation
ax2 + bx + c = 0
is given by the expression
b2 − 4ac
It provides critical information about the roots of the equation: if the discriminant is positive, the equation has two distinct real roots; if it is zero, there is one real root (a repeated root); and if it is negative, the equation has two complex roots. Discriminant visualization helps in understanding these scenarios graphically, showing how the parabola interacts with the x-axis. In real-world applications, the discriminant is used in engineering and physics to determine the stability of systems and the feasibility of solutions. In math education, the discriminant is a key concept for solving quadratic equations and analyzing their graphs. It aids students in predicting the number and type of solutions without graphing, enhancing their problem-solving skills. An example of using the discriminant is in the equation
x2 + 2x + 1 = 0
where the discriminant is zero, indicating a repeated root at x = −1.
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms |