Display Title
Definition--Quadratics Concepts--Increasing Quadratic Function
Display Title
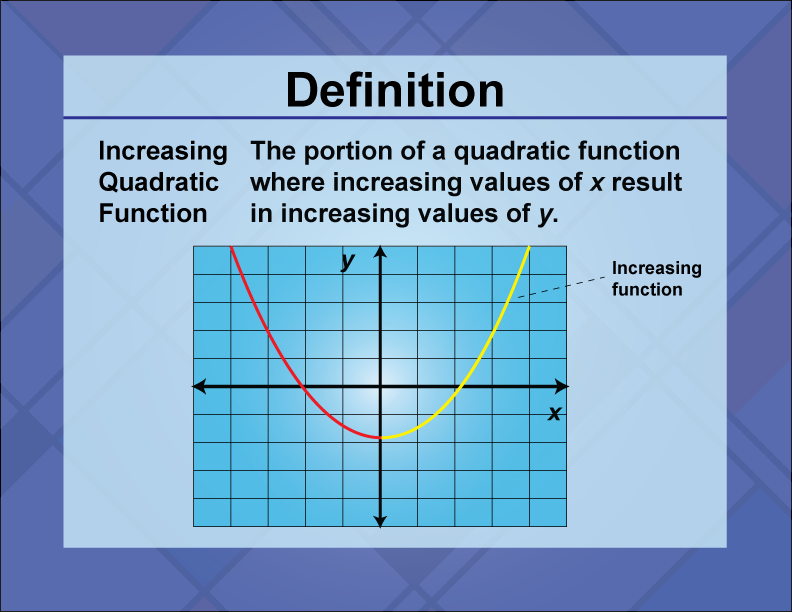
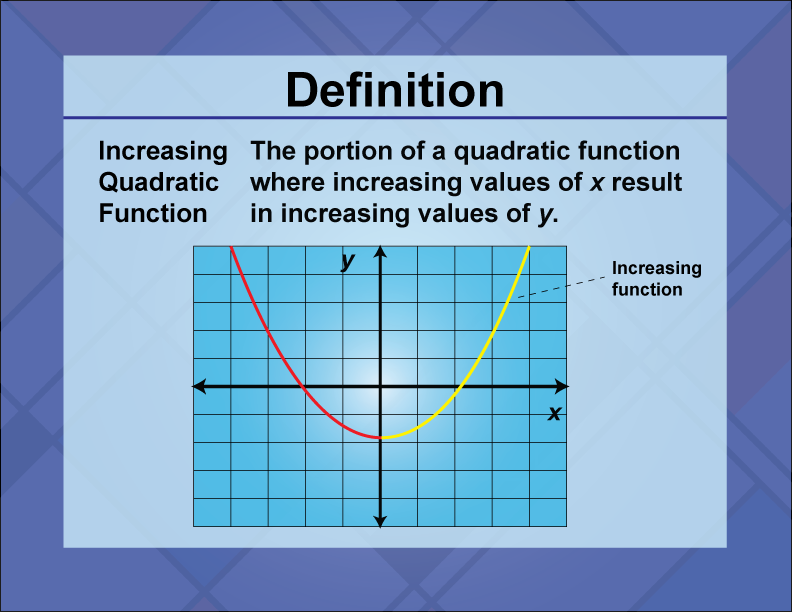
Increasing Quadratic Function
Topic
Quadratics Concepts
Definition
An increasing quadratic function is a parabola that opens upward, indicating that its vertex is a minimum point.
Description
An increasing quadratic function is characterized by a leading coefficient that is positive, resulting in a parabola that opens upward. This means that as the input values increase, the output values increase after reaching a minimum at the vertex. The standard form of such a function is
f(x) = ax2 + bx + c
with a>0. Increasing quadratic functions are used in real-world applications to model scenarios where a quantity decreases to a minimum and then increases, such as the cost of production decreasing to a minimum before rising. In math education, understanding increasing quadratic functions is important for analyzing function behavior, graphing parabolas, and solving optimization problems. Students learn to identify the vertex as the minimum point and use it to determine the range of the function.
An example of an increasing quadratic function is
f(x) = 2x2 − 4x + 1
where the vertex is the minimum point of the parabola.
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms |