Display Title
Definition--Quadratics Concepts--Maximum
Display Title
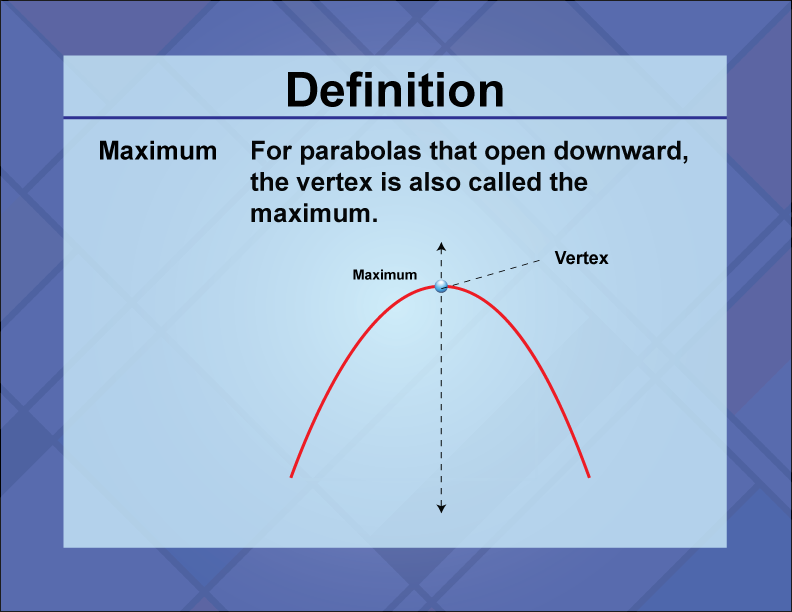
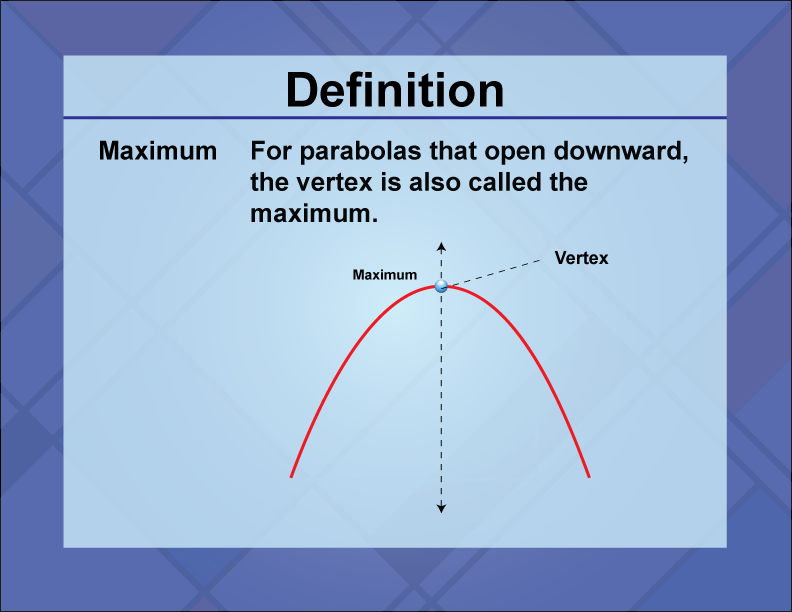
Maximum
Topic
Quadratics Concepts
Definition
The maximum of a quadratic function is the highest point on its graph, occurring at the vertex when the parabola opens downward.
Description
The maximum of a quadratic function is an important concept in understanding the behavior of parabolas. When a quadratic function is in the form
f(x) = −ax2 + bx + c
with a > 0, the parabola opens downward, and the vertex represents the maximum point. This maximum value is crucial in optimization problems, where determining the highest value of a function is necessary, such as maximizing profit or efficiency. In math education, learning about the maximum of quadratic functions helps students analyze and graph parabolas, solve real-world problems, and understand the significance of the vertex in determining function behavior. An example of finding the maximum is in the function
f(x) = −x2 + 4x + 5
where the vertex and maximum point is (2, 9).
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms |