Definition--Quadratics Concepts--Parabola
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Quadratic Functions and Equations >> Quadratic Equations and Functions

Definition--Quadratics Concepts--Parabola

Parabola

Parabola Image

Topic

Quadratics Concepts

Definition

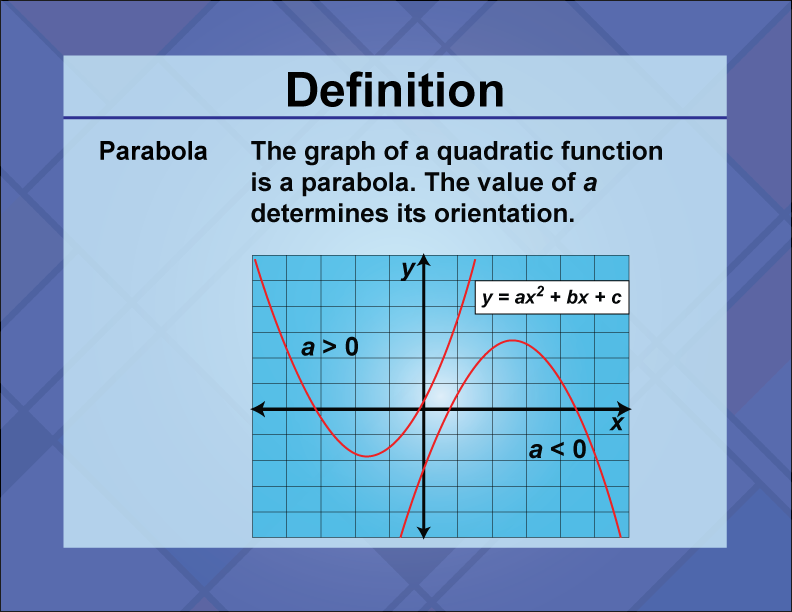
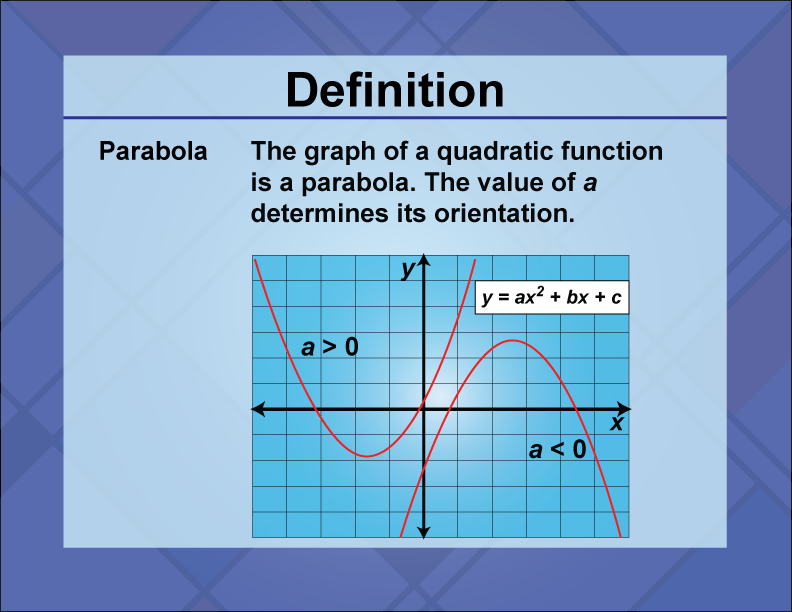
A parabola is a U-shaped curve that is the graph of a quadratic function.

Description

The parabola is a fundamental concept in the study of quadratic functions, representing the graph of the equation 

y = ax2 + bx + c

It is characterized by its symmetric shape, with a vertex as its highest or lowest point, depending on whether it opens upward or downward. Parabolas are used in various real-world applications, including physics (projectile motion), engineering (design of reflective surfaces), and economics (cost and revenue functions). In math education, understanding parabolas is crucial for graphing quadratic functions, solving quadratic equations, and exploring the properties of conic sections. Students learn to identify key features such as the vertex, axis of symmetry, and intercepts, which are essential for analyzing and interpreting quadratic graphs. 

An example of a parabola is the graph of 

y = x2 − 4x + 3

which is a U-shaped curve opening upward.

For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection

Common Core Standards CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A
Grade Range 6 - 10
Curriculum Nodes Algebra
    • Quadratic Functions and Equations
        • Quadratic Equations and Functions
Copyright Year 2013
Keywords quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms