Display Title
Definition--Quadratics Concepts--Vertex
Display Title
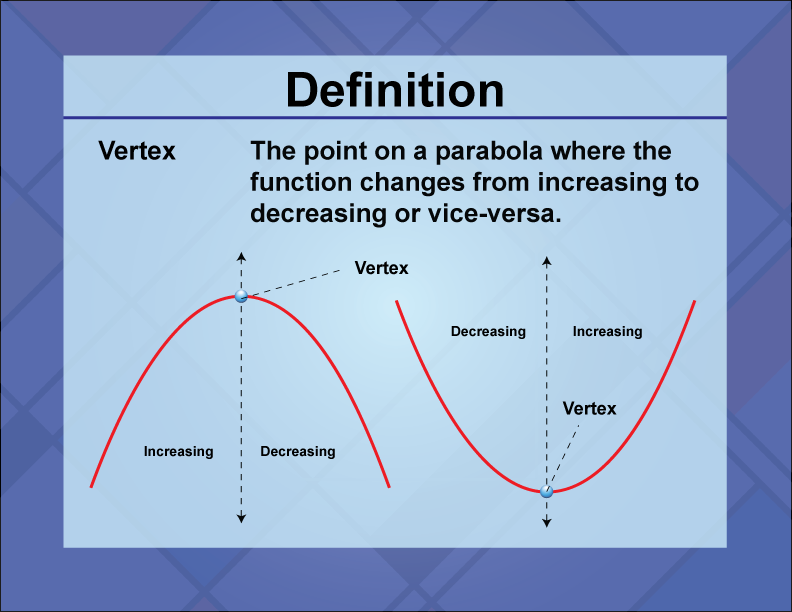
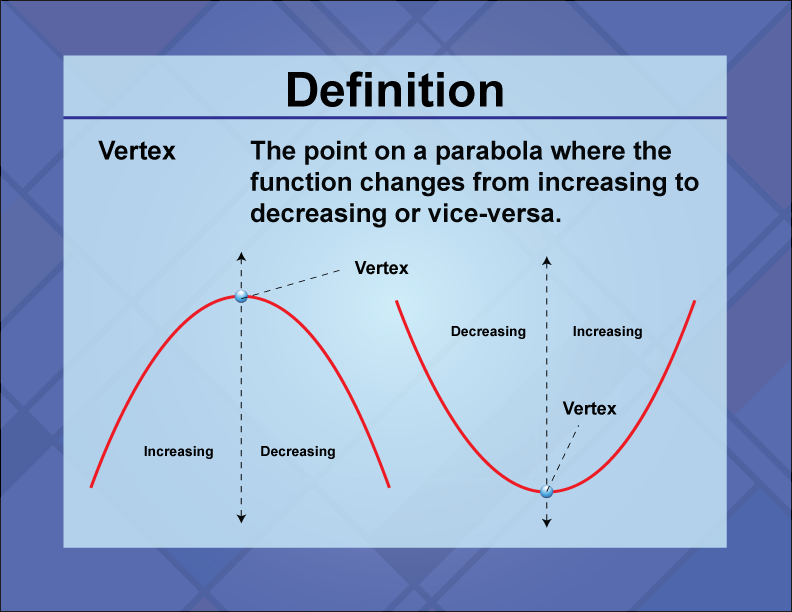
Vertex
Topic
Quadratics Concepts
Definition
The vertex of a parabola is the point where the parabola changes direction, representing the maximum or minimum value of the quadratic function.
Description
The vertex is a crucial feature of a quadratic function, providing the highest or lowest point on the graph, depending on whether the parabola opens upward or downward. It is determined by the formula (h, k), where h = − b/(2a) k is the function evaluated at h. In real-world applications, the vertex is used in optimization problems to find maximum or minimum values, such as in maximizing profit or minimizing cost. In math education, understanding the vertex helps students analyze and graph quadratic functions, solve problems, and comprehend the significance of the vertex in determining function behavior. By identifying the vertex, students learn to interpret the graph and use it to make predictions and solve problems. An example of finding the vertex is in the function
f(x) = x2 − 4x + 3
where the vertex is at (2, −1).
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms |