Display Title
Definition--Rationals and Radicals--Horizontal Asymptote
Display Title
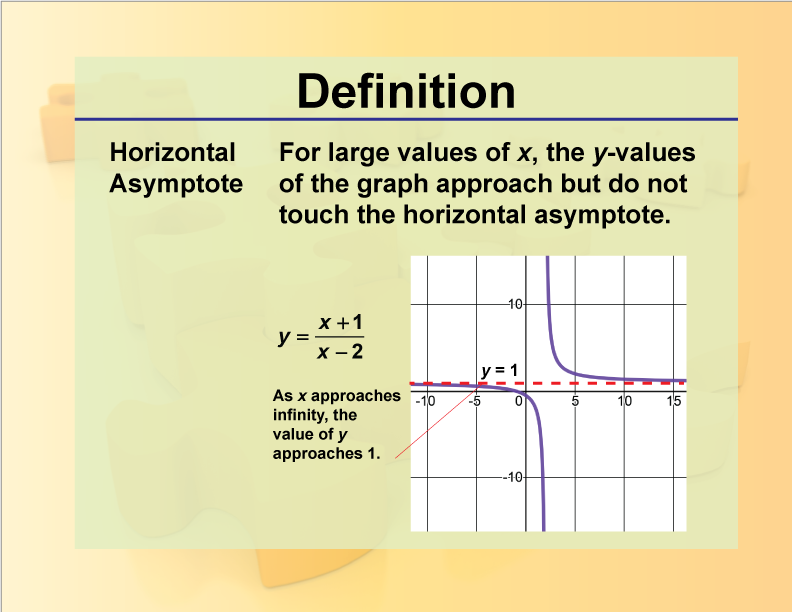
Horizontal Asymptote

Topic
Rationals and Radicals
Definition
A horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small.
Description
Horizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior.
These asymptotes also play a role in calculus, where they help in understanding limits and the end behavior of functions. They are essential for solving equations involving rational expressions and for performing various algebraic manipulations.
For a complete collection of terms related to polynomials click on this link: Rationals and Radicals Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.A.2, CCSS.MATH.CONTENT.HSN.RN.A.1, CCSS.MATH.CONTENT.HSF.IF.C.7 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2022 |
| Keywords | radicals, radical expressions, rational numbers, rational expressions, definitions, glossary term, rational functions |