Display Title
Definition--Rationals and Radicals--Vertical Asymptote
Display Title
Vertical Asymptote

Topic
Rationals and Radicals
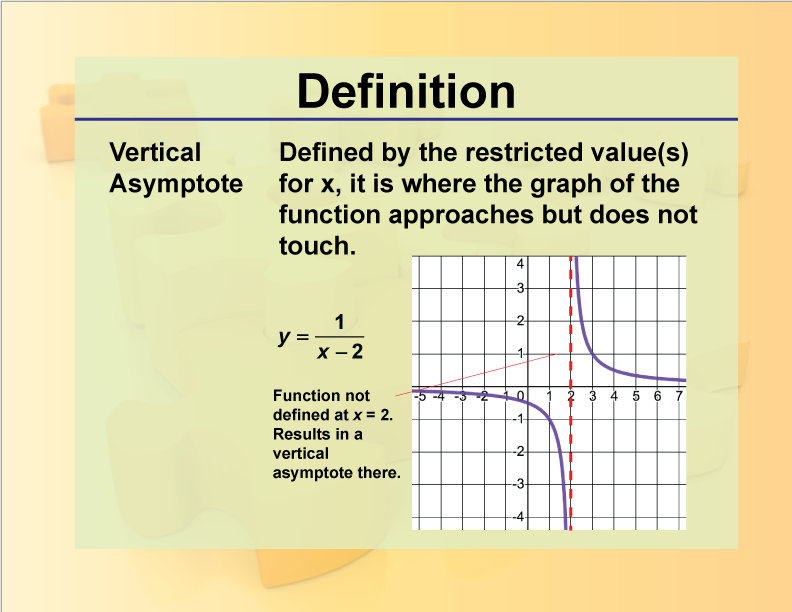
Definition
A vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point.
Description
Vertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function
f(x)=1x−2
has a vertical asymptote at x = 2. Understanding vertical asymptotes is essential for analyzing the behavior of rational functions and their graphs. Vertical asymptotes provide important information about the domain of a function and its behavior near certain points. They indicate where the function is undefined and where its values become arbitrarily large in magnitude. This concept is particularly important in calculus when studying limits and continuity of functions.
In practical applications, vertical asymptotes are used to model various phenomena in physics, engineering, and economics. For instance, they can represent situations where a quantity grows rapidly as it approaches a certain point, such as the force between two charged particles as they get very close to each other. In financial modeling, vertical asymptotes can represent scenarios where costs or profits change dramatically under certain conditions. Understanding vertical asymptotes helps students develop a deeper comprehension of function behavior and graphing techniques. It enhances their ability to analyze and interpret graphs, which is a valuable skill in many fields of study and professional areas. This concept also introduces students to the idea of discontinuities in functions, preparing them for more advanced topics in mathematics such as complex analysis and differential equations. By mastering the concept of vertical asymptotes, students improve their problem-solving skills and their ability to model real-world situations mathematically.
For a complete collection of terms related to polynomials click on this link: Rationals and Radicals Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.A.2, CCSS.MATH.CONTENT.HSN.RN.A.1, CCSS.MATH.CONTENT.HSF.IF.C.7 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2022 |
| Keywords | radicals, radical expressions, rational numbers, rational expressions, definitions, glossary term, rational functions |