Display Title
Definition--Triangle Concepts--3-4-5 Right Triangle
Display Title
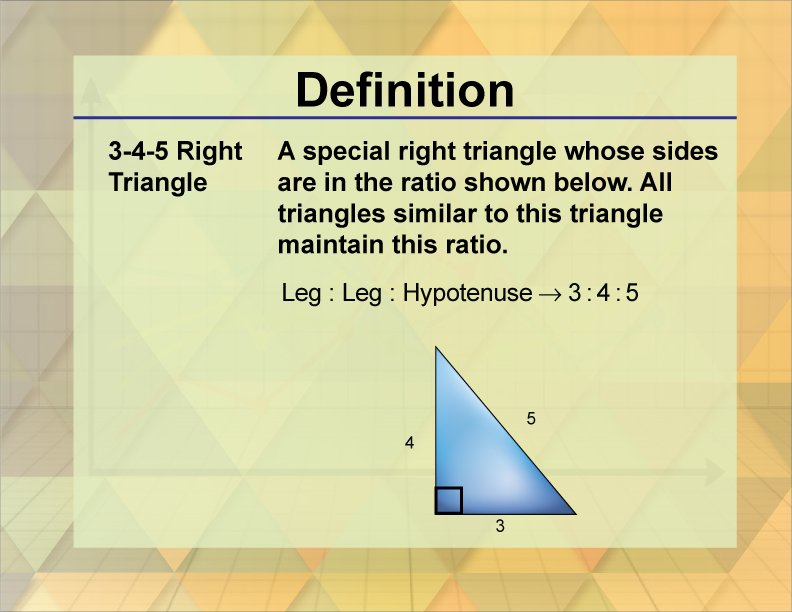
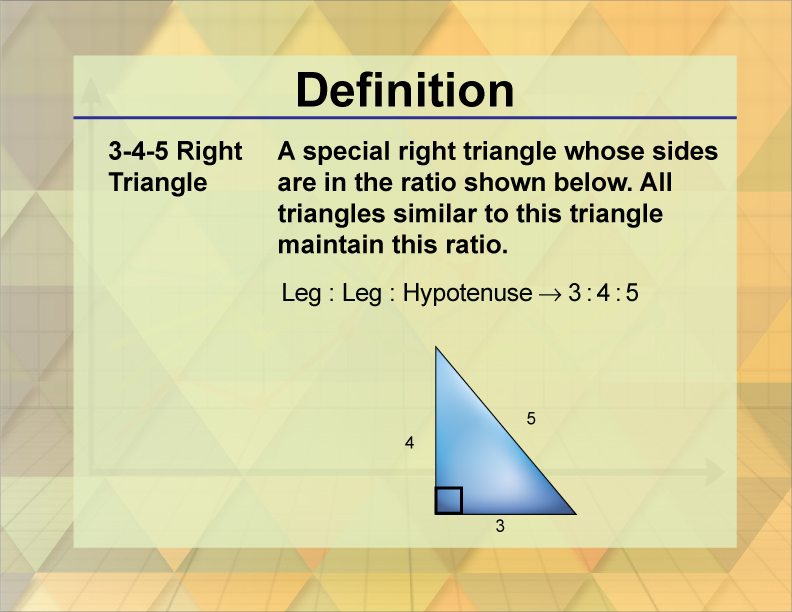
3-4-5 Right Triangle
Topic
Triangles
Definition
A 3-4-5 right triangle is a right triangle with side lengths in the ratio 3:4:5.
Description
The 3-4-5 right triangle is a specific type of right triangle where the sides are in a simple integer ratio, making it a Pythagorean triple. This triangle is significant in geometry because it provides a simple example of the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides:
32 + 42 = 52
In real-world applications, the 3-4-5 triangle is often used in construction and carpentry to ensure right angles. For example, if a builder needs to create a right angle, they can measure 3 units along one side, 4 units along the adjacent side, and if the diagonal measures 5 units, they have a right angle. This practical use of the 3-4-5 triangle helps ensure accuracy in building projects.
Understanding the 3-4-5 triangle is crucial in math education as it provides a tangible example of the Pythagorean theorem and helps students grasp the concept of right triangles and their properties. By working with this specific triangle, students can better understand the relationships between the sides of right triangles and apply these principles to more complex problems.
For a complete collection of terms related to functions and relations click on this link: Triangles Collection
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.1, CCSS.MATH.CONTENT.7.G.A.2, CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Definition of a Triangle |
| Copyright Year | 2013 |
| Keywords | triangle, defnitions, glossary |