Display Title
Definition--Triangle Concepts--Centroid of a Triangle
Display Title
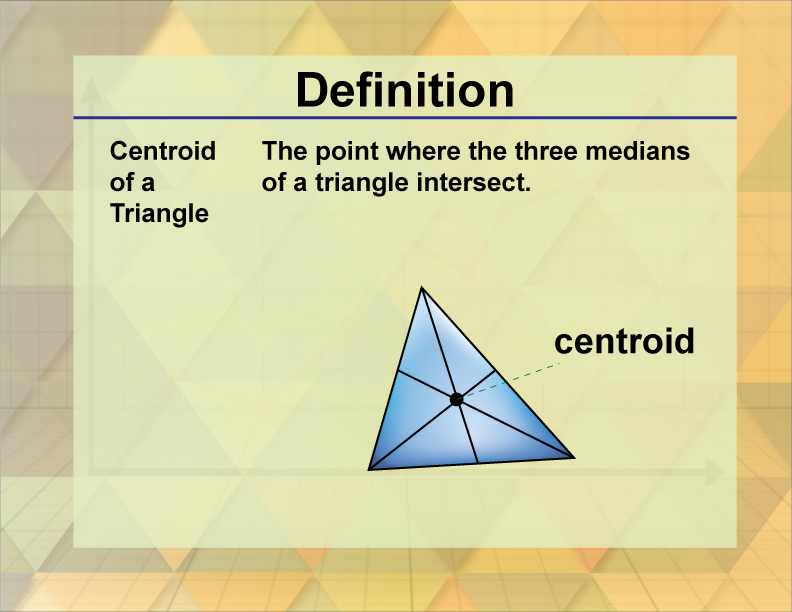
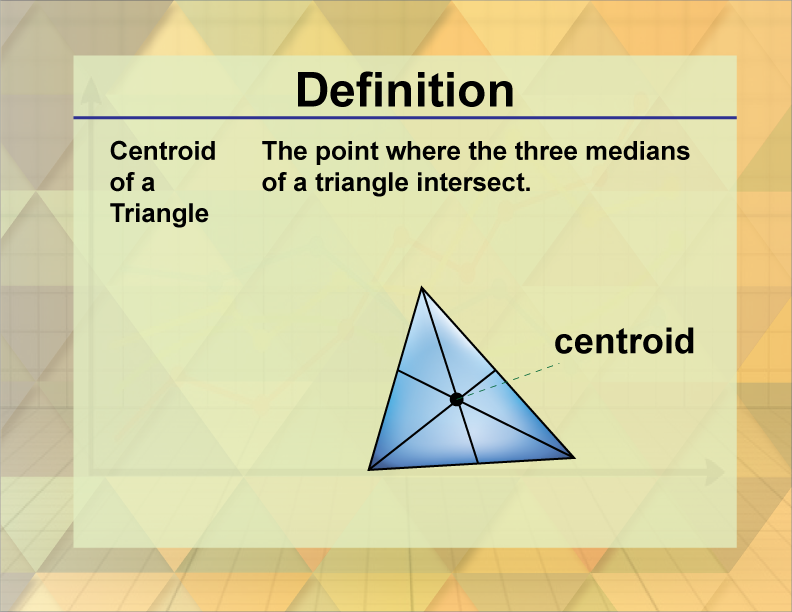
Centroid of a Triangle
Topic
Triangles
Definition
The centroid of a triangle is the point where its three medians intersect, often considered the triangle's center of mass.
Description
The centroid of a triangle is a significant point in geometry, representing the intersection of the triangle's medians. Each median is a line segment drawn from a vertex to the midpoint of the opposite side. The centroid is also known as the triangle's center of mass or balance point.
This concept is essential in various real-world applications, such as in engineering and design. For example, understanding the centroid helps in determining the center of mass of triangular components, which is crucial for stability and balance in structures. In physics, the centroid is used to analyze the distribution of mass and forces within a triangular object.
In math education, learning about the centroid helps students understand the broader concepts of geometry and the properties of triangles. It also provides a foundation for more advanced topics, such as coordinate geometry and calculus. By mastering this concept, students can apply their knowledge to solve practical problems and develop a deeper understanding of geometric principles.
For a complete collection of terms related to functions and relations click on this link: Triangles Collection
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.1, CCSS.MATH.CONTENT.7.G.A.2, CCSS.MATH.CONTENT.4.G.A.2 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Definition of a Triangle |
| Copyright Year | 2021 |
| Keywords | triangle, defnitions, glossary |