Display Title
Definition--Triangle Concepts--Circumcenter of a Triangle
Display Title
Circumcenter of a Triangle
Topic
Triangles
Definition
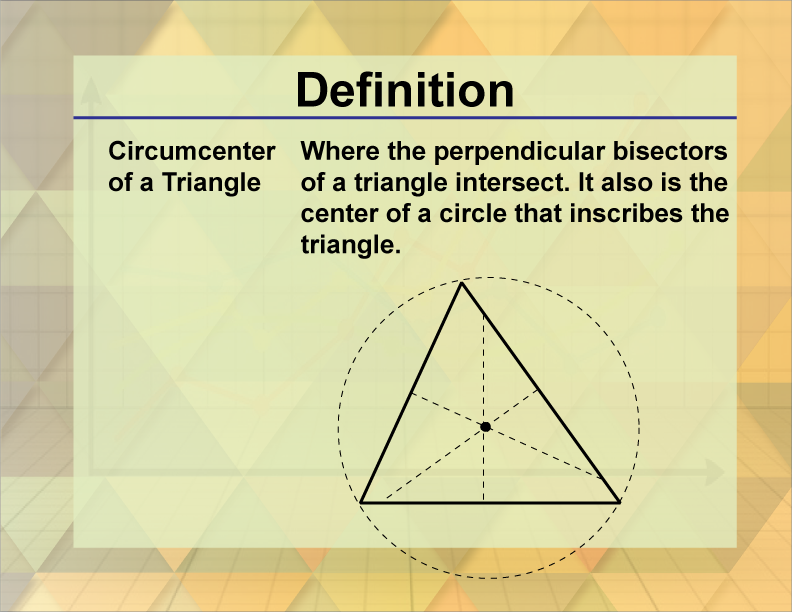
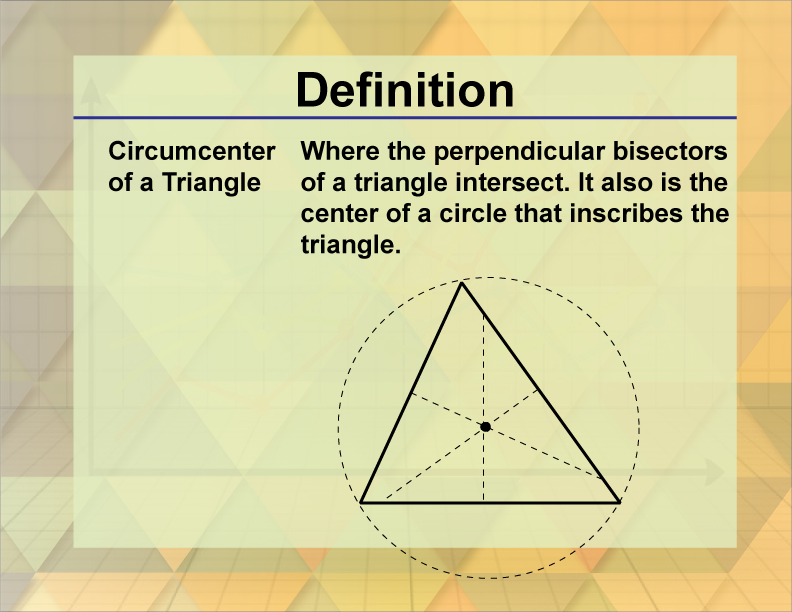
The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, and it is the center of the triangle's circumcircle.
Description
The circumcenter of a triangle is a crucial concept in geometry, representing the point where the perpendicular bisectors of the triangle's sides intersect. This point is equidistant from all three vertices of the triangle, making it the center of the circumcircle, which is the circle that passes through all three vertices.
This concept is essential in various real-world applications, such as in navigation and design. For example, understanding the circumcenter helps in determining the optimal location for placing a circular object that needs to be equidistant from three points. In navigation, the circumcenter can be used to triangulate positions and ensure accuracy.
In math education, learning about the circumcenter helps students understand the broader concepts of geometry and the properties of triangles. It also provides a foundation for more advanced topics, such as coordinate geometry and calculus. By mastering this concept, students can apply their knowledge to solve practical problems and develop a deeper understanding of geometric principles.
For a complete collection of terms related to functions and relations click on this link: Triangles Collection
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.1, CCSS.MATH.CONTENT.7.G.A.2, CCSS.MATH.CONTENT.4.G.A.2 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Definition of a Triangle |
| Copyright Year | 2013 |
| Keywords | triangle, defnitions, glossary |