Display Title
Definition--Triangle Concepts--Perimeter of a Triangle
Display Title
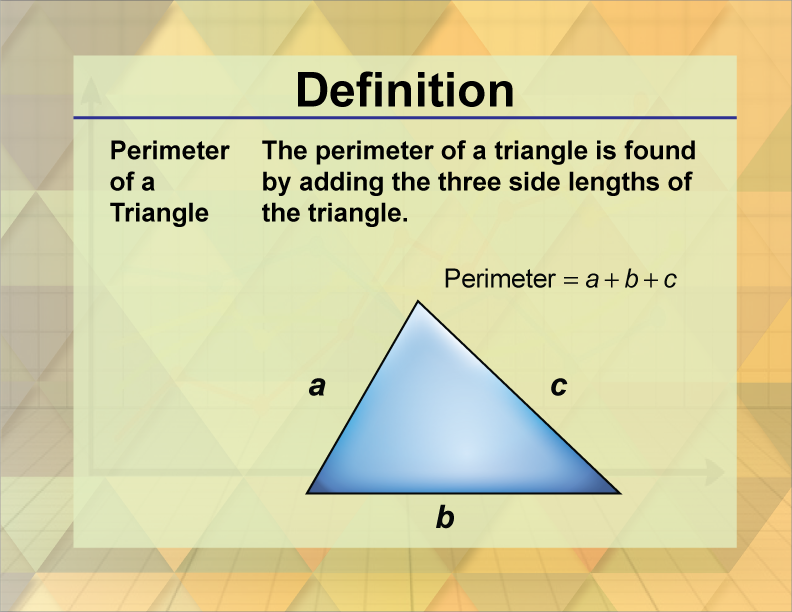
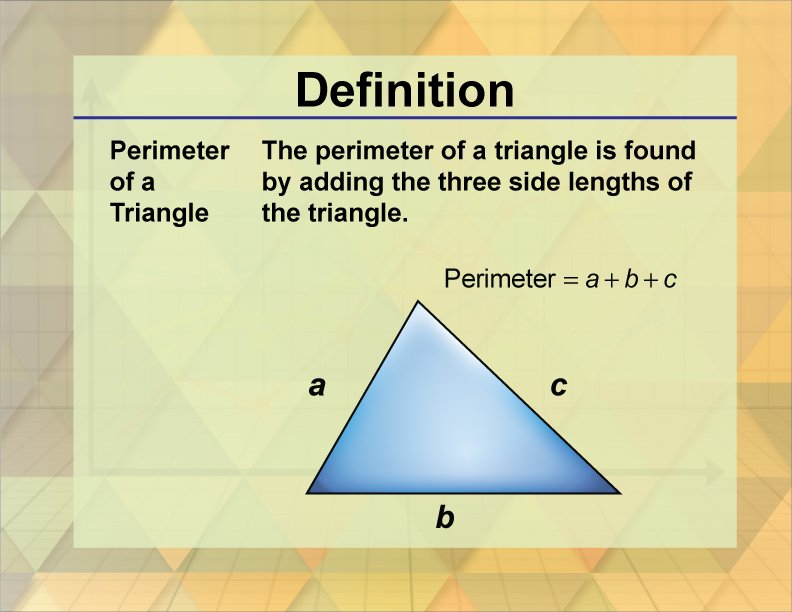
Perimeter of a Triangle
This is part of a collection of definitions on the topic of Triangles. This downloadable collection of definitions can easily be incorporated into a lesson plan.
—PRESS PREVIEW TO SEE THE DEFINITION—
To see the complete collection of definitions on this topic, click on this link.
The following section includes background information on the general topic of perimeter and specifically on the perimeter of a triangle.
Brief Review of Triangle Perimeter
Watch this video to learn about triangle perimeter. (The video transcript is also available.)
The Perimeter of a Triangle
The video was uploaded on 9/9/2022.
You can view the video here.
The video lasts for 1 minute and 25 seconds.
Video Transcript
The perimeter of a geometric shape is the length around it.
The perimeter can be made up of line segments or curves.
When a set of line segments meet end to end to form a closed figure, then they form a polygon.
A polygon with three sides is a triangle.
So the perimeter of a triangle is the sum of the lengths of the sides.
Let's look at some examples.
This triangle has side lengths of 3, 5, and 7.
The perimeter of this triangle is shown here.
3 + 5+ 7 = 15
This triangle has side lengths with decimal values.
The perimeter is the sum of these decimals, as shown here.
Sometimes a triangle has a variable for a side length, like this.
The perimeter is this algebraic expression.
Suppose you know that the perimeter of this triangle is 20.
How can you find the value for x?
You can write this equation, with the algebraic expression for the perimeter on the left and the known value of the perimeter on the right.
This forms an equation that can be solved.
Solve for x.
Brief Review of Perimeter
The perimeter of a geometric shape is the distance around it.
For now, let's just look at the perimeter of a polygon. Take a look at this polygon and make a note of the measurements of the side lengths.
Simply add the side lengths to find the perimeter:
P = 3 + 2 + 3 + 6 + 4
= 17
Perimeter of a Triangle
A triangle is a type of polygon. It has three sides. The perimeter of a triangle is the sum of the lengths of the three sides. Here’s an example.
Simply add the side lengths to find the perimeter:
P = 3 + 6 + 4
= 13
Sometimes a triangle has side lengths that are variables. Take a look at this triangle.
Simply add the side lengths to find the perimeter:
Perimeters of Special Triangles
Finding the perimeter with certain types of triangles can be easier. For example, consider an isosceles triangle.
Notice that two of the sides have the same length. Here’s how to calculate the perimeter of an isosceles triangle:
Perimeter = 2•7 + 5
= 14 + 5
= 19
An equilateral triangle has three equal sides. Look at the following equilateral triangle. Notice that the perimeter is simply 3 times the length of one of the sides.
P = 3 • 9
= 27
Right triangles have two legs and a hypotenuse. Because of the Pythagorean Theorem, there is a relationship between the legs and sides. Use that to find the perimeter of the triangle, as shown below.
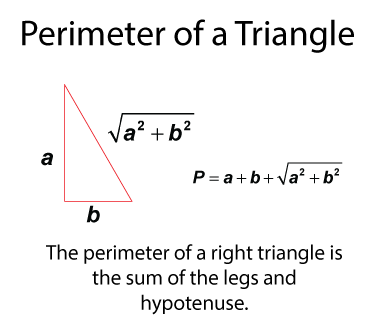
Perimeters of Similar Triangles
When two triangles are similar, their sides are proportional. How does this affect the perimeter? Take at look at these two similar triangle:
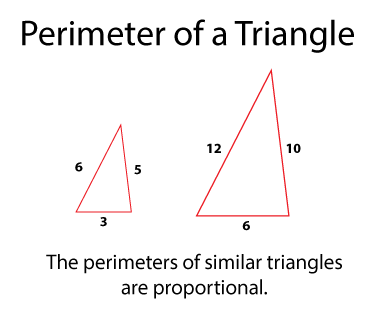
Notice that corresponding sides are in a 2:1 ratio. For example, the base of the smaller triangle is 3 and the base of the larger triangle is twice that. The same ratio holds for the other two corresponding sides. How does this affect the perimeters? This table shows the perimeter calculators for each triangle:
P = 3 + 6 + 5= 14 |
P = 6 + 12 + 10= 28 |
Notice that the perimeters are also in the 2:1 ratio.
Solving Perimeter Equations
There are cases where you know the perimeter and need to find the side length. For example, here is a triangle-shaped garden. It is the in the shape of an isosceles triangle with a perimeter of 50 ft. How can you use the information provided to find the side lengths labeled x.
We know that the perimeter of an isosceles triangle has this equation. The 2x term results from the fact that two of the sides of an isosceles triangle are congruent.
P = 2x + 10
Simply plug in the value for the perimeter and solve for x:
50 = 2x + 10
2x = 40
x = 20
The downloadable image is part of a collection of definitions related to triangles and related concepts. This includes general definitions for triangles and triangle properties, as well as specific triangle types. Relationships among different types of triangles are also defined.
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math definitions on this topic. To see the complete collection of definitions, click on this Link.
To learn more about Slide Show Creator, click on this Link:
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.
-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.
-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.1, CCSS.MATH.CONTENT.7.G.A.2, CCSS.MATH.CONTENT.4.G.A.2 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Definition of a Triangle |
| Copyright Year | 2013 |
| Keywords | triangle, defnitions, glossary |