Display Title
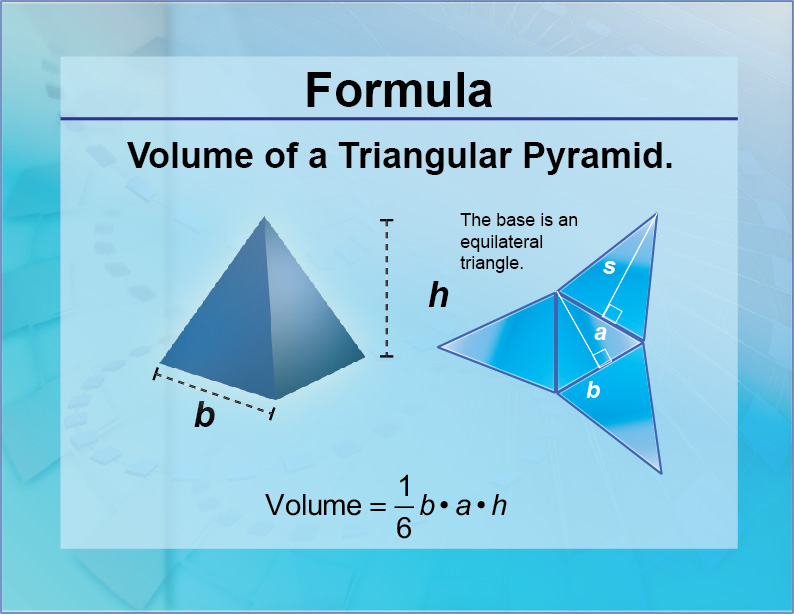
Formulas--Volume of a Triangular Pyramid
Display Title
Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.)
Video Transcript
Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance.
Mathematically, pyramids also have an air of mystery. Let’s take a closer look.
Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward.
Here is a square pyramid with the same base and height as the cube. Yet, its volume is 1/3 s-cubed. Now, we know that it has less volume than the cube just by comparing the two.
But one third? Where does this fractional amount come from? To derive the formula for the volume of a pyramid is not as straightforward as finding the volume of the cube, but it will reveal some of the mysteries of pyramids.
Let’s start exploring the volume of a pyramid using cubes. As we build these pyramids, we’ll use a grid to show an overhead view of the base of the pyramid, as well as a 3D view with the cubes.
As we build these pyramids, we’ll make sure that as the base expands, the height of the pyramid grows accordingly, because we’ll be comparing the volumes of the pyramids we build to similar-sized cubes. Let’s start.
Here is a pyramid with a 2 by 2 base. This is the overhead view, and this is the stack of cubes. Because its base is two, the pyramid has two levels. So there is a single cube at the top. This is a very simple pyramid.
What is the volume of this pyramid? Count the cubes: 1-2-3-4-5 cubic units. A cube with a 2 by 2 base has a volume of 8, which is the same as 2-cubed.
This table captures the volume of the pyramid, 5; the volume of the corresponding cube, 8; and most important, the ratio of the pyramid’s volume to the cube’s volume, 5/8.
Let’s add more cubes.
Here is a pyramid with a 3 by 3 base. Here is the overhead view of the base and here are the cubes stacked to three levels.
This table shows the volume of the pyramid, 14; the volume of a 3 by 3 cube, which is 27; and the ratio of the volumes, 14/27.
Here is a pyramid with a 4 by 4 base. The table summarizes the volume of the pyramid, 30; the volume of the cube, 64; and the ratio (in simplest form), 15/32.
Finally, here is a pyramid with a 5 by 5 base. The table summarizes the volume of the pyramid, 55; the volume of the cube, 125; and the ratio (in simplest form), 11/25.
This bar graph shows the ratios for the four pyramids we constructed. Notice what happens to the ratios as the number of cubes increases. You can see how the ratio is approaching the baseline value of 1/3.
So this is our first indication that the volume of the pyramid is around one third the volume of the cube. Let’s look at it another, more precise way.
With this grid, we’ll look at the pyramid from the side. Here is the three-tier pyramid we constructed. The volume of the corresponding cube is 3-cubed. But here’s another way of looking at the volume of the pyramid. Each level is a square base, so the volume of the pyramid is 3-squared, for the base; 2-squared for level 2; and 1-squared (or 1) for the top layer.
Here is the four-tier pyramid. The volume of the cube is 4-cubed. The volume of the pyramid is 4-squared, for the base layer; 3-squared for the second tier; 2-squared for the third tier; and 1-squared (or 1) for the top layer.
See a pattern?
Here is a generalized pyramid that is n cubes wide and n cubes tall. We know the volume of the cube is n-cubed.
What about the volume of the pyramid? As you’ve seen, it’s the sum of square terms from n = 1 to n. This is summarized by this formula, which uses the summation symbol, Sigma.
This is where things get interesting.
It turns out this summation formula can be written as an explicit formula. The explicit formula for this sequence is shown here.
Let’s use the explicit formula for the volume of the pyramid to look at the ratio of the volume of the pyramid to the volume of the cube. We end up with this rational expression.
Let’s break up the ratio into three parts, as shown here. We end up with three terms, 1/3 plus 1 over 2n plus 1 over 6-n-squared.
Now, what happens as the value of n increases? That means that our pyramid goes from a jagged stairstep to a smooth pyramid. And this happens as n approaches an infinitely large value.
But as n approaches infinity, what happens to these terms? They get infinitely small, as they approach zero. This means that as n approaches infinity the ratio of the volume of the pyramid to the ratio of the cube is the one third term we saw earlier.
Now we’ve come full circle and see how the volume of a pyramid is one third the area of the base times the height. This one third term is the result of an infinite series.
Infinity is a mathematical concept but it often gets tangled up with divinity, so is it any wonder that pyramids have religious connections? From the Egyptians who used pyramids as sacred tombs to the Mayans who used pyramids as celestial calendars, pyramids have a built in geometry of mystery.
The downloadable image is part of a collection of mathematical formulas.
Related Resources
To see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas
| Common Core Standards | CCSS.MATH.CONTENT.6.G.A.2, CCSS.MATH.CONTENT.HSG.GMD.A.1, CCSS.MATH.CONTENT.HSG.GMD.A.2, CCSS.MATH.CONTENT.HSG.GMD.A.3, CCSS.MATH.CONTENT.HSG.GMD.B.4 |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Geometry • Surface Area and Volume • Volume |
| Copyright Year | 2013 |
| Keywords | volume, triangular pyramid, formulas |