Display Title
Math Clip Art--Applications of Linear Functions: Temperature Conversion 08
Display Title
Math Clip Art--Applications of Linear Functions: Temperature Conversion 08
Topic
Linear Functions
Description
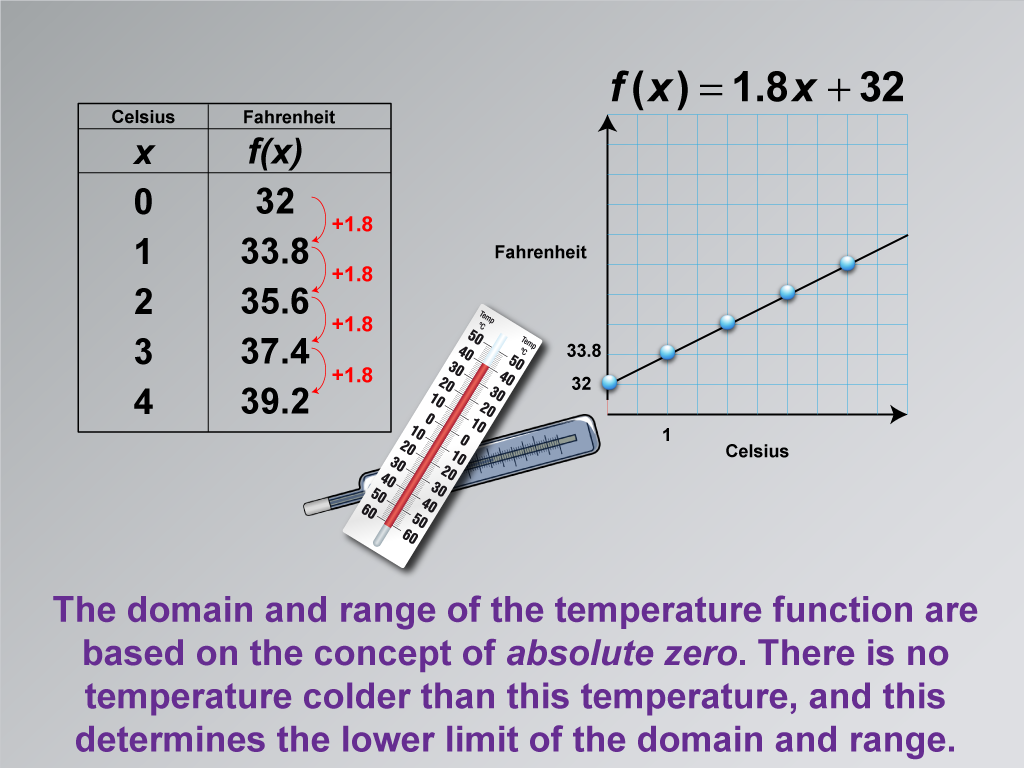
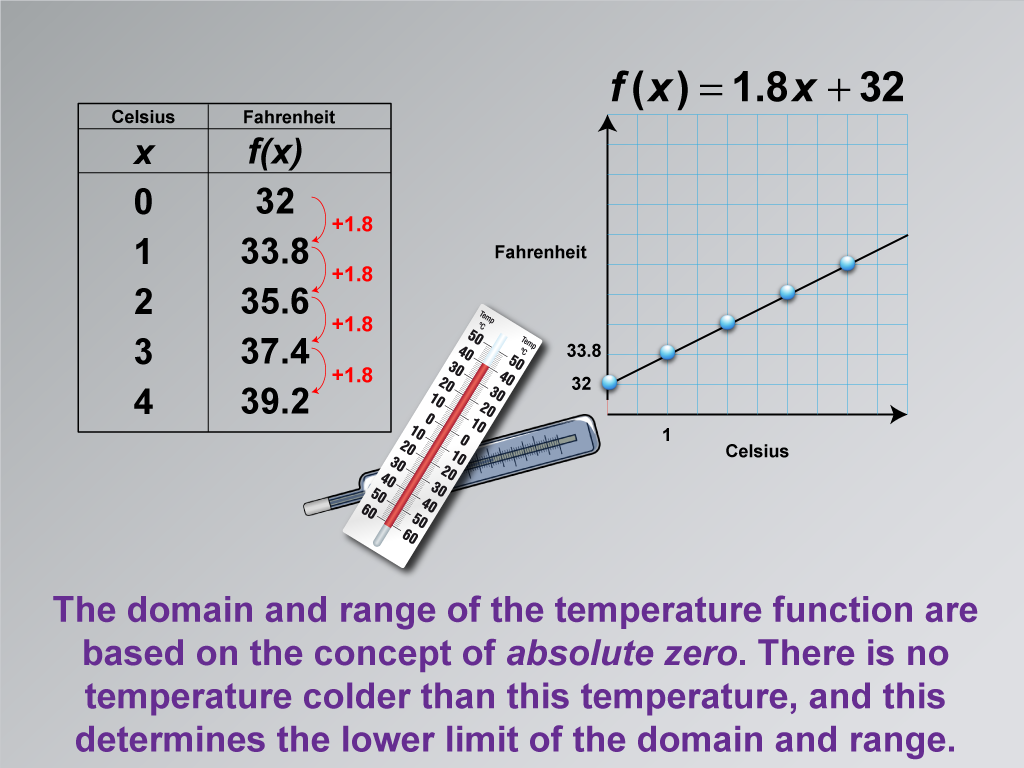
This image delves deeper into the concept of domain and range in the context of temperature conversion. It explains that the limits of the temperature function are based on the concept of absolute zero, the lowest theoretically possible temperature. This fundamental principle of physics determines the lower bounds of both the domain and range of the temperature conversion function.
By connecting the mathematical concept of domain and range to the physical concept of absolute zero, this image helps students understand how real-world constraints shape mathematical models. It illustrates that while linear functions can extend infinitely in theory, practical applications often have defined limits.
Using math clip art in this way is particularly effective in teaching linear functions. It not only reinforces mathematical concepts but also integrates knowledge from other scientific disciplines, promoting interdisciplinary understanding. This approach helps students appreciate the broader applications and limitations of mathematical models in real-world scenarios.
A teacher might introduce this image by saying: "Remember the domain and range we discussed? Let's explore why these specific values are important. Have you heard of absolute zero? It's the coldest possible temperature in the universe. How does this physical concept affect our mathematical model for temperature conversion? Why can't our function extend below these values?"
For a complete collection of math clip art related to Applications of Linear Functions click on this link: Applications of Linear Functions: Temperature Conversion Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.2, CCSS.MATH.CONTENT.8.F.A.3, CCSS.MATH.CONTENT.HSF.LE.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Graphs of Linear Functions • Slope-Intercept Form |
| Copyright Year | 2021 |
| Keywords | linear functions |