Display Title
Math Clip Art--Applications of Linear Functions: Temperature Conversion 09
Display Title
Math Clip Art--Applications of Linear Functions: Temperature Conversion 09
Topic
Linear Functions
Description
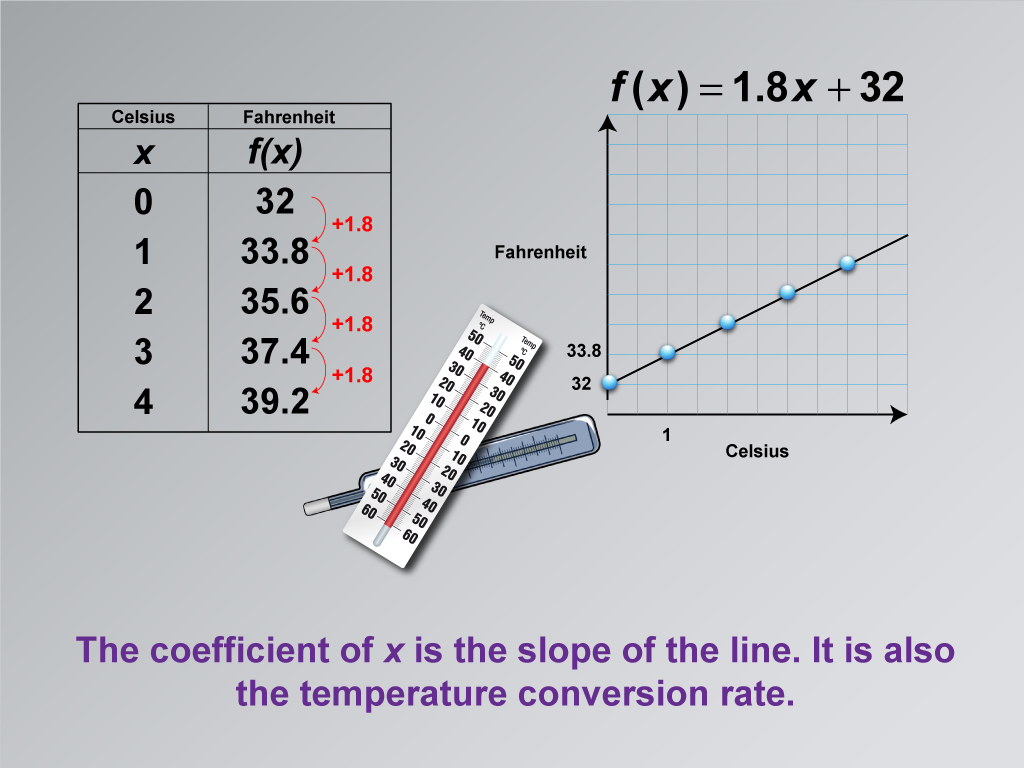
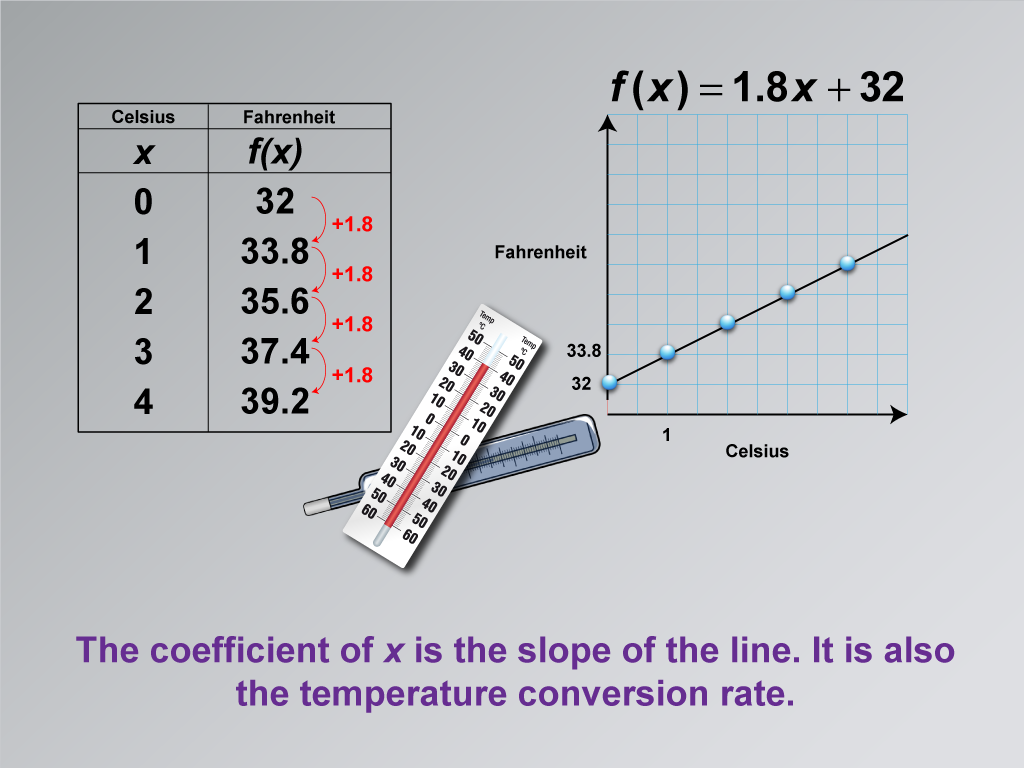
This final image in the series on applications of linear functions in temperature conversion focuses on the significance of the coefficient of x in the linear equation. It emphasizes that this coefficient, 1.8 in the equation f(x) = 1.8x + 32, represents both the slope of the line and the temperature conversion rate.
By highlighting the dual meaning of this coefficient, the image reinforces the connection between the graphical representation of the linear function (where slope is visually apparent) and its algebraic form. This helps students understand that the rate of change in a linear function is constant and is represented by the slope of the line.
Incorporating such math clip art into lessons on linear functions is highly effective. It provides a clear, visual way to connect multiple aspects of linear functions - the equation, the graph, and the real-world application. This comprehensive approach helps solidify students' understanding of how different representations of a linear function relate to each other and to practical scenarios.
A teacher might introduce this image by saying: "Let's take a closer look at the number 1.8 in our equation. We've seen it before in our data and our graph. Can you explain what this number represents in terms of the line on our graph? How does it relate to converting temperatures? This coefficient is key to understanding both the mathematical and practical aspects of our temperature conversion function."
For a complete collection of math clip art related to Applications of Linear Functions click on this link: Applications of Linear Functions: Temperature Conversion Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.2, CCSS.MATH.CONTENT.8.F.A.3, CCSS.MATH.CONTENT.HSF.LE.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Graphs of Linear Functions • Slope-Intercept Form |
| Copyright Year | 2021 |
| Keywords | linear functions |