Display Title
Math Clip Art--Function Concepts--Function Graphs 05
Display Title
Math Clip Art--Function Concepts--Function Graphs 05
Topic
Functions
Description
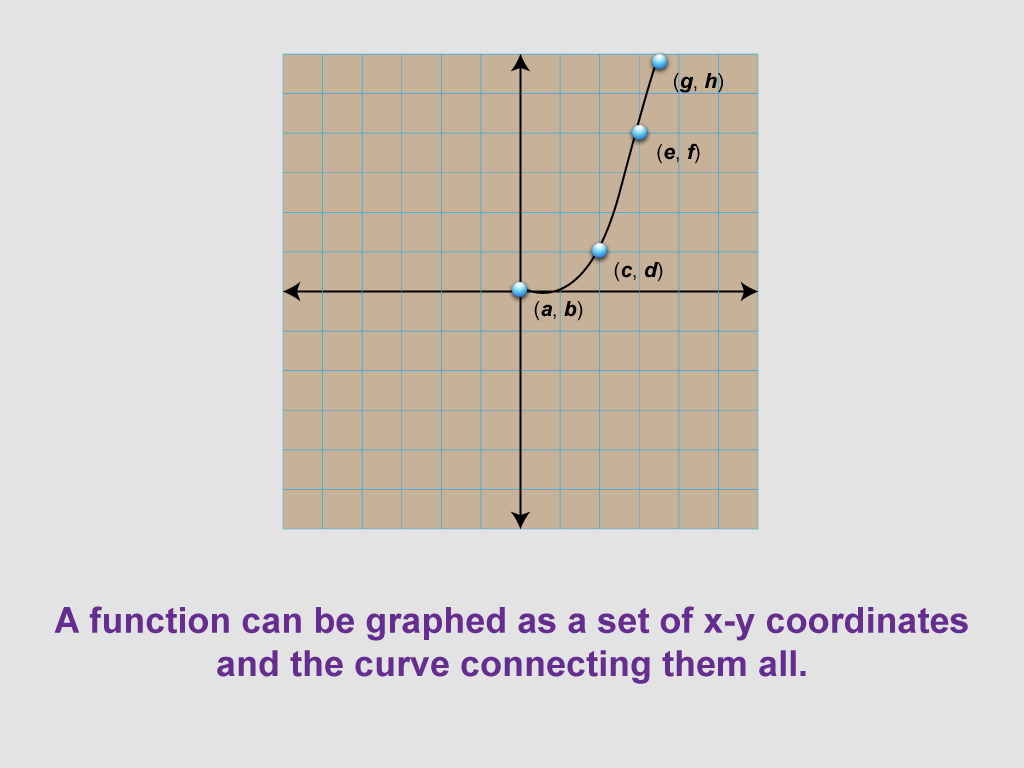
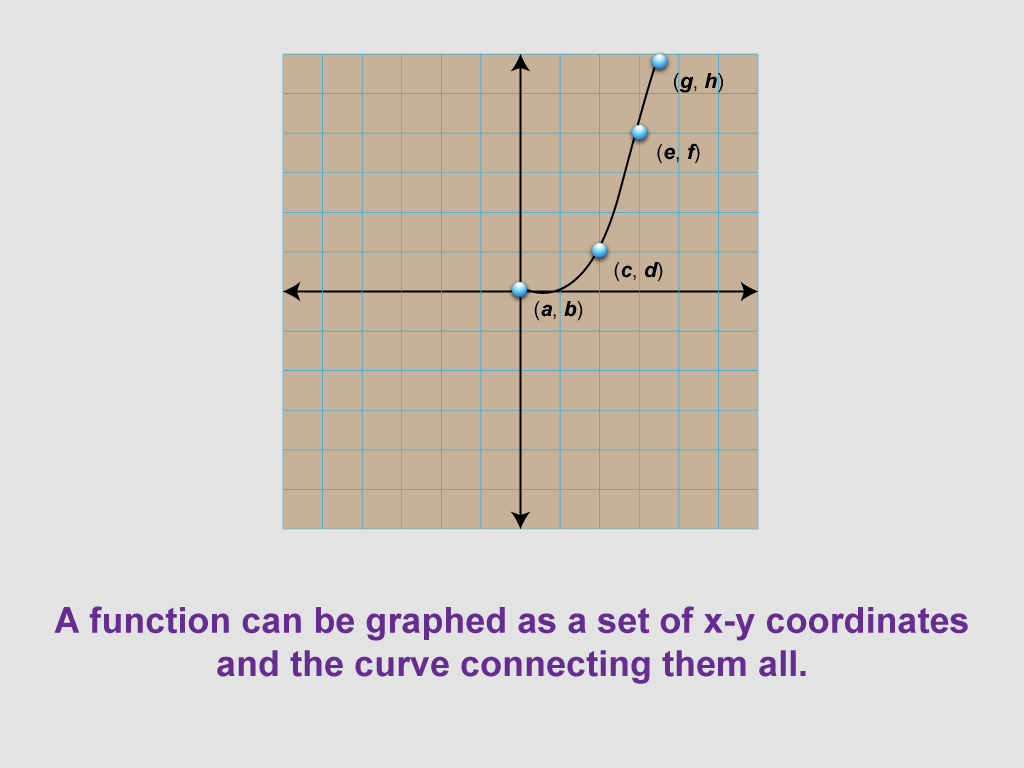
This image shows a grid with a curve passing through four points labeled (a, b), (c, d), (e, f), and (g, h). It demonstrates that a function can be graphed as a set of x-y coordinates with a curve connecting them all, representing a non-linear function.
The curved line passing through all the labeled points introduces the concept of non-linear functions. This visualization helps students understand how a continuous curve can represent a function, with each point on the curve corresponding to an input-output pair. It's an excellent tool for discussing various types of non-linear relationships, such as quadratic, exponential, or logarithmic functions.
Using this type of visual representation allows educators to emphasize the diverse nature of functions. Students can learn to identify key features of non-linear functions, such as turning points, concavity, and asymptotes. This image provides an opportunity to discuss how the rate of change varies along a curve, contrasting with the constant rate of change in linear functions. It also sets the stage for more advanced topics like calculus, where the behavior of curves is analyzed in detail.
Teacher's Script: "Now we see a curve passing through our labeled points. How does this differ from the straight line we saw earlier? What can you say about the rate of change as we move along this curve? Let's discuss what types of real-world phenomena might be better modeled by a curve like this rather than a straight line."
For a complete collection of math clip art related to Function Graphs click on this link: Function Graphs Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.8, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2020 |
| Keywords | functions |