Display Title
Math Clip Art: Parallel Lines Cut by a Transversal 16
Display Title
Math Clip Art: Parallel Lines Cut by a Transversal 16
Topic
Geometry
Description
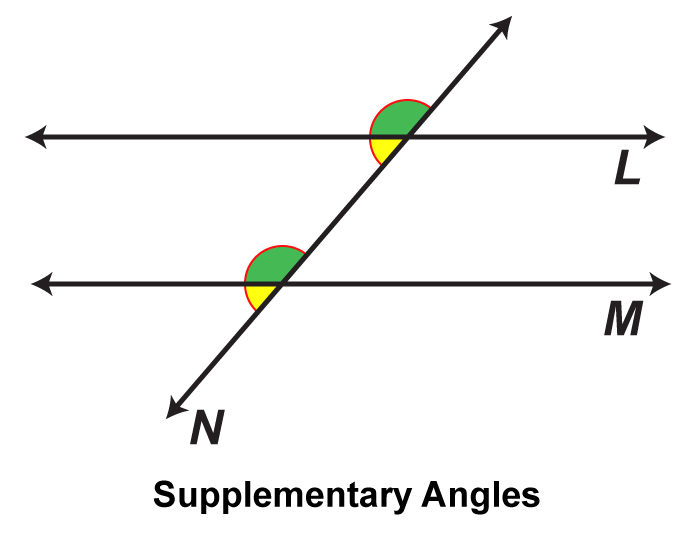
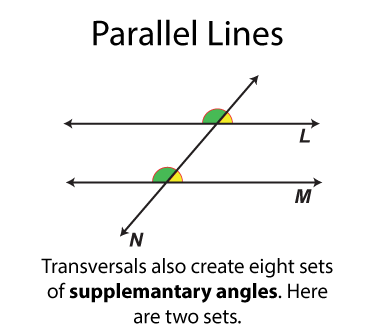
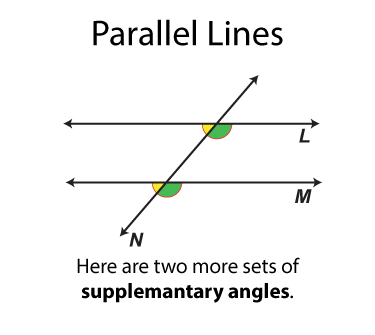
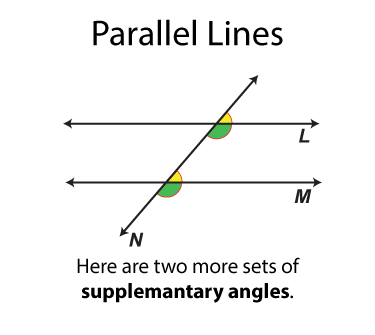
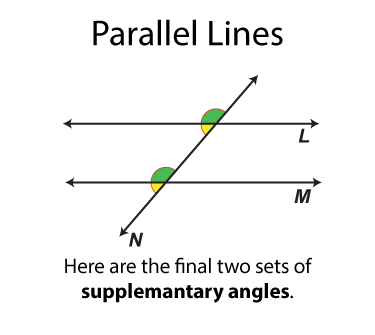
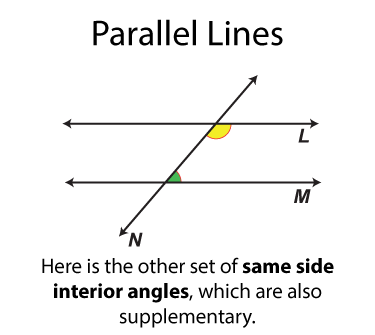
This math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It showcases a fourth pair of supplementary angles, reinforcing the concept that certain pairs of angles formed by parallel lines and a transversal are supplementary (their measures add up to 180°). The image uses distinct color coding to identify this pair of supplementary angles, providing students with a comprehensive view of all possible supplementary angle pairs in this configuration.
Using math clip art like this in geometry lessons can significantly enhance students' understanding of spatial relationships. The multiple visual representations of supplementary angles help students internalize this concept more effectively than verbal explanations alone. This image can be easily integrated into lessons on geometry, serving as a culminating visual aid for reinforcing the concept of supplementary angles in the context of parallel lines cut by a transversal.
Teacher's Script: "With this final pair of supplementary angles, we've now seen all four pairs in this configuration. Notice how each pair adds up to 180°, regardless of its position. This consistency is a fundamental property of parallel lines cut by a transversal. Let's discuss how we can use this knowledge to solve more complex geometric problems. Can you think of a real-world scenario where understanding supplementary angles might be useful, perhaps in architecture or engineering?"
For a complete collection of math clip art related to Geometry click on this link: Parallel Lines Cut by a Transversal Collection.
Parallel Lines Cut by a Transversal
Parallel lines are on the same plane and do not intersect. Here are two lines, L and M, that are on plane P and parallel.
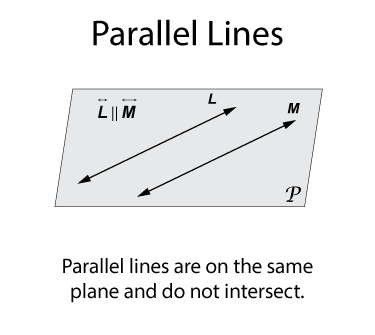
Parallel lines are are always the same distance from each other. In this illustration the dashed segment indicates the distance between the two lines. That distance doesn't change.
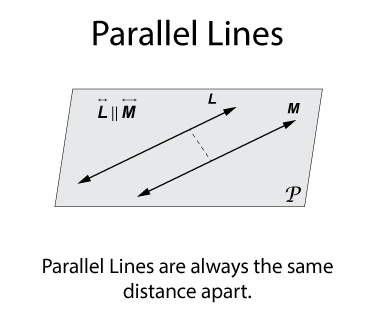
A line that intersects the parallel lines is called a transversal. In the illustration below you can see transveral N that insersects lines L and M.
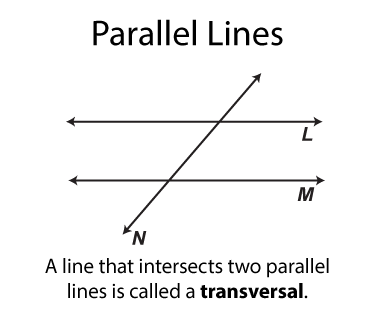
When parallel lines are cut by a transversal, there are number of set of angles whose properties are important to remember. The categories of angles include:
- Alternate interior angles
- Alternate exterior angles
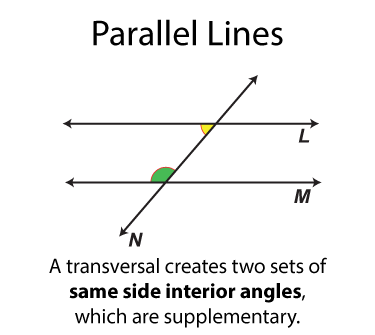
- Same side interior angles
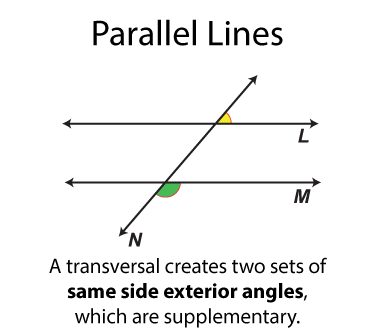
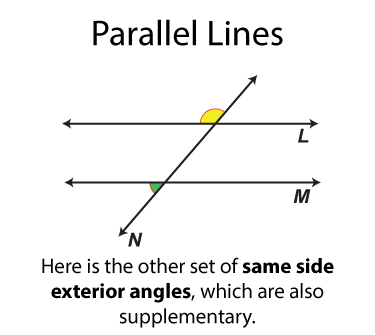
- Same side exterior angles
- Supplementary angles
- Vertical angles
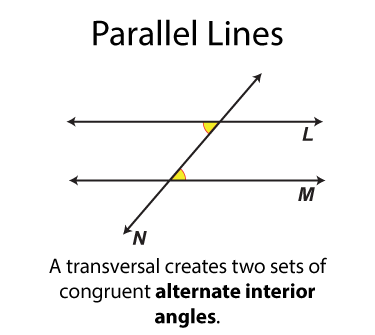
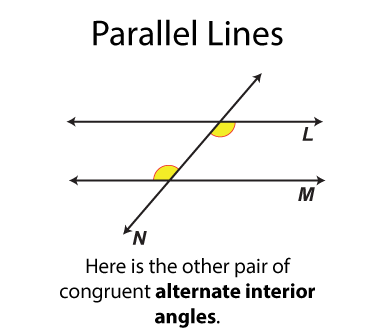
Let's start with the alternate interior angles, which are shown here. There are two sets of alternate interior angles. These pairs of angles are congruent. The word "alternate" means "opposite" In each case the one angle is on the opposite side of the transversal from the other angle.
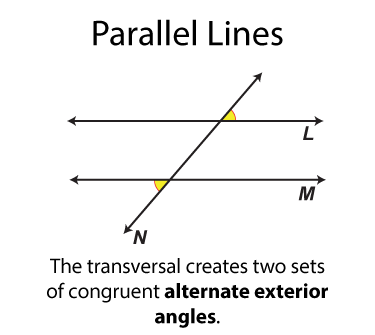
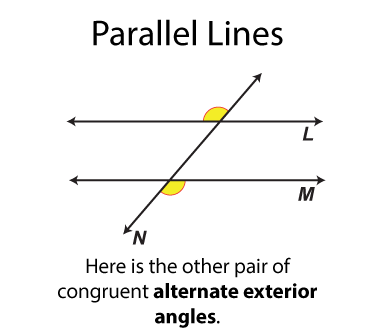
The next set of angles are called alternate exterior angles. There are two sets. Each set of angles is congruent. Each angle is on one side of the transversal from the other angle it is congruent to.
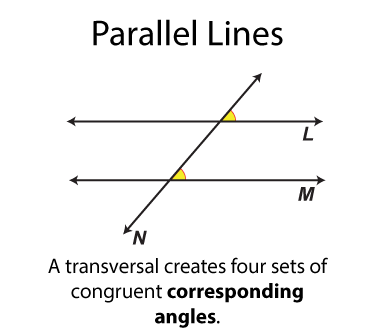
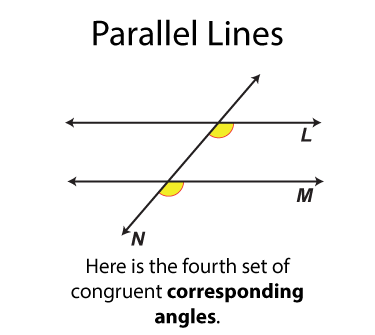
The next set of angles are called corresponding angles. There are four sets. Each set of angles is congruent. Each set of angles is on the same side of the transversal.
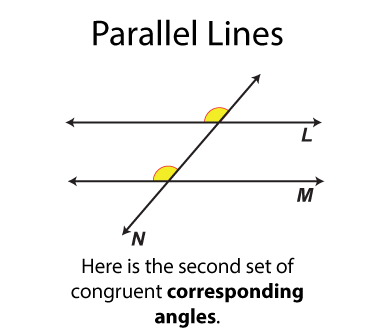
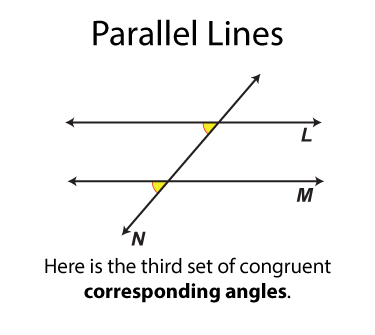
The next set of angles are called vertical angles. There are two sets. Each set of angles is congruent. (By definition all vertical angles are congruent.) Each angle is on on the opposite side of the transversal from the other angle it is congruent to.
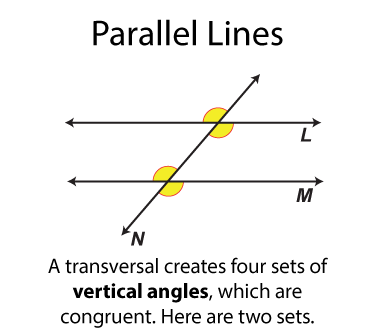
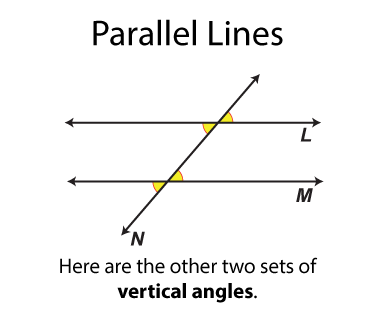
The next set of angles are called vertical angles. There are two sets. Each set of angles is congruent. (By definition all vertical angles are congruent.) Each angle is on on the opposite side of the transversal from the other angle it is congruent to.


The next set of angles are supplementary angles. There are eight sets. By definition the supplementary angles add up to 180°. Some pairs of supplementary angles are on opposite sides of the transversal and some are on the same side.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines |
| Copyright Year | 2020 |
| Keywords | Parallel Lines Cut by a Transversal, parallel lines, transversal, vertical angles, supplementary angles, alternate interior angles, alternate exterior angles |