Display Title
Math Example: Absolute Value Functions: Example 3
Display Title
Math Example: Absolute Value Functions: Example 3
Topic
Special Functions
Description
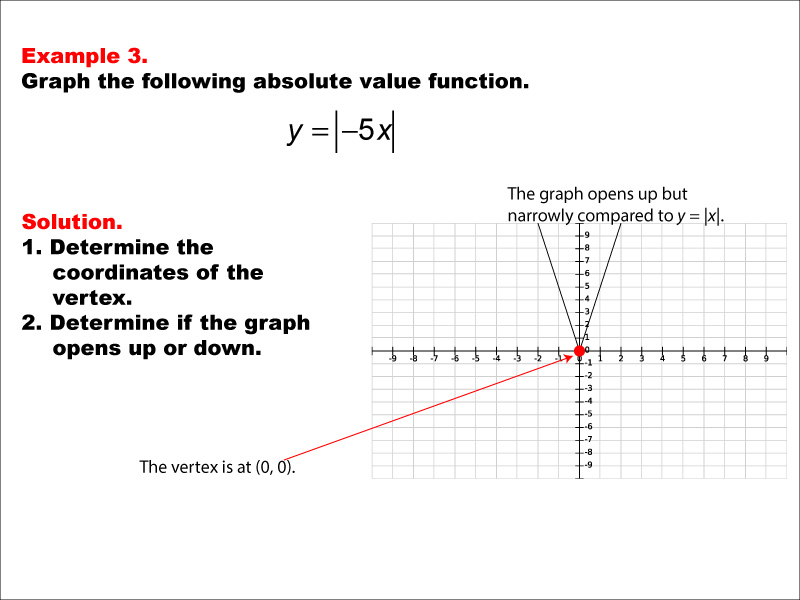
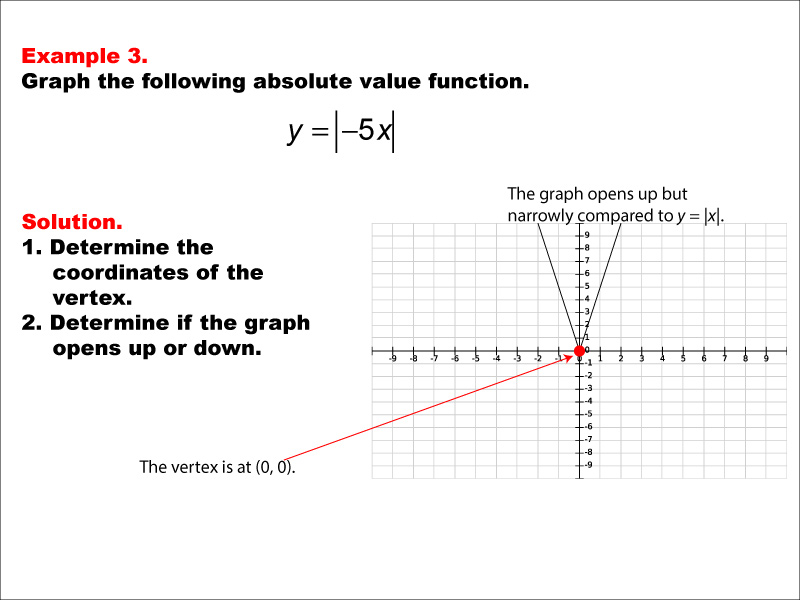
This image displays a graph of y = |-5x|, showing a V-shape that is narrower than y = abs(x), opening upwards from the origin (0, 0). This example demonstrates how a negative coefficient with an absolute value greater than 1 affects the function. The graph is steeper and narrower than the basic form, but still opens upwards due to the absolute value operation. It illustrates that the sign of the coefficient inside the absolute value doesn't change the direction of the graph's opening. Absolute value functions are an important concept in algebra, introducing students to equations that involve taking the absolute value of a variable or expression. This collection of examples showcases various forms of absolute value functions, allowing students to observe how changes in the equation impact the resulting graph's shape, steepness, and orientation. Providing multiple worked-out examples is crucial for students to fully comprehend the concept of absolute value functions. By examining different scenarios, students can identify patterns and develop a deeper understanding of how these functions behave. This approach helps reinforce important concepts such as the characteristic V-shape of absolute value graphs, the impact of coefficients (both positive and negative) on the graph's steepness, and how vertical and horizontal shifts affect the function's appearance. Through repeated exposure to diverse examples, students can build intuition and improve their ability to analyze and graph absolute value functions independently.
For a complete collection of math examples related to Special Functions: Absolute Value Functions click on this link: Math Examples: Special Functions: Absolute Value Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Special Functions |
| Copyright Year | 2013 |
| Keywords | function, graph, vertex, vertices |