Display Title
Math Example: Absolute Value Functions: Example 7
Display Title
Math Example: Absolute Value Functions: Example 7
Topic
Special Functions
Description
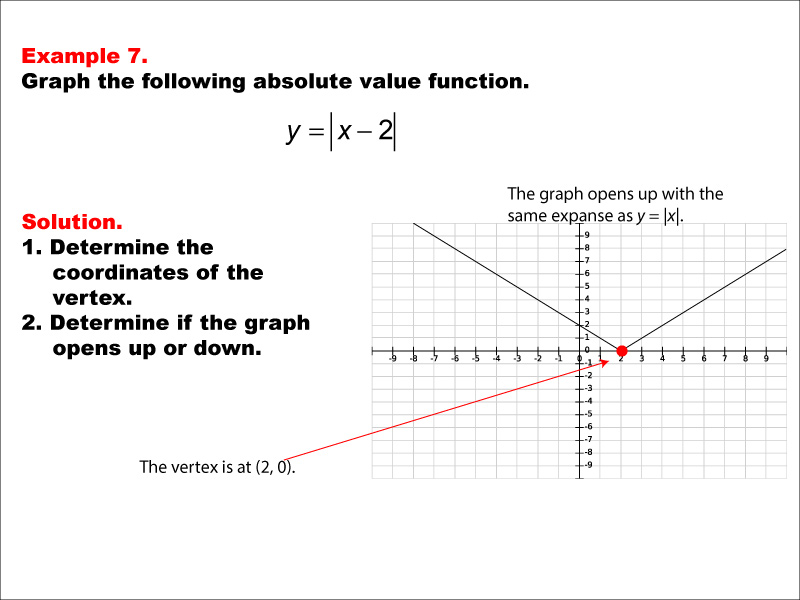
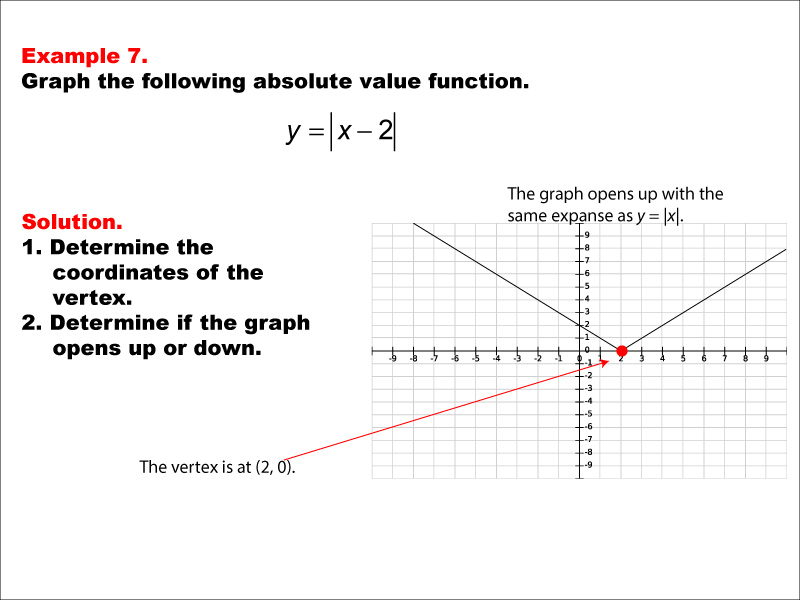
The image shows a graph of the absolute value function y = |x - 2|. The graph is a V-shape opening upwards with the vertex at (2, 0). This example demonstrates how subtracting a constant inside the absolute value affects the graph's horizontal position. The V-shape is shifted 2 units to the right compared to the basic form, illustrating the concept of horizontal translation in absolute value functions. Absolute value functions are a fundamental concept in algebra, introducing students to equations that involve taking the absolute value of a variable or expression. This collection of examples showcases various forms of absolute value functions, allowing students to observe how changes in the equation impact the resulting graph's shape, position, and orientation. Providing multiple worked-out examples is essential for students to fully comprehend the concept of absolute value functions. By examining different scenarios, students can identify patterns and develop a deeper understanding of how these functions behave. This approach helps reinforce important concepts such as the characteristic V-shape of absolute value graphs, the impact of constants inside the absolute value on the graph's horizontal position, and how vertical and horizontal shifts affect the function's appearance. Through repeated exposure to diverse examples, students can build intuition and improve their ability to analyze and graph absolute value functions independently.
For a complete collection of math examples related to Special Functions: Absolute Value Functions click on this link: Math Examples: Special Functions: Absolute Value Functions Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7.B |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Algebra • Functions and Relations • Special Functions |
| Copyright Year | 2013 |
| Keywords | function, graph, vertex, vertices |