Display Title
Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 13
Display Title
Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 13
Topic
Angles
Description
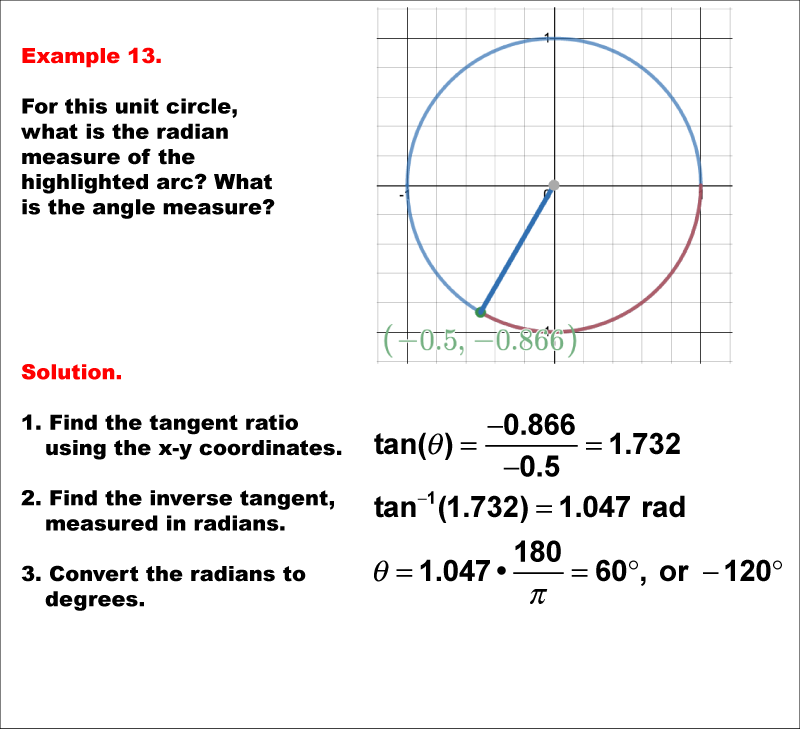
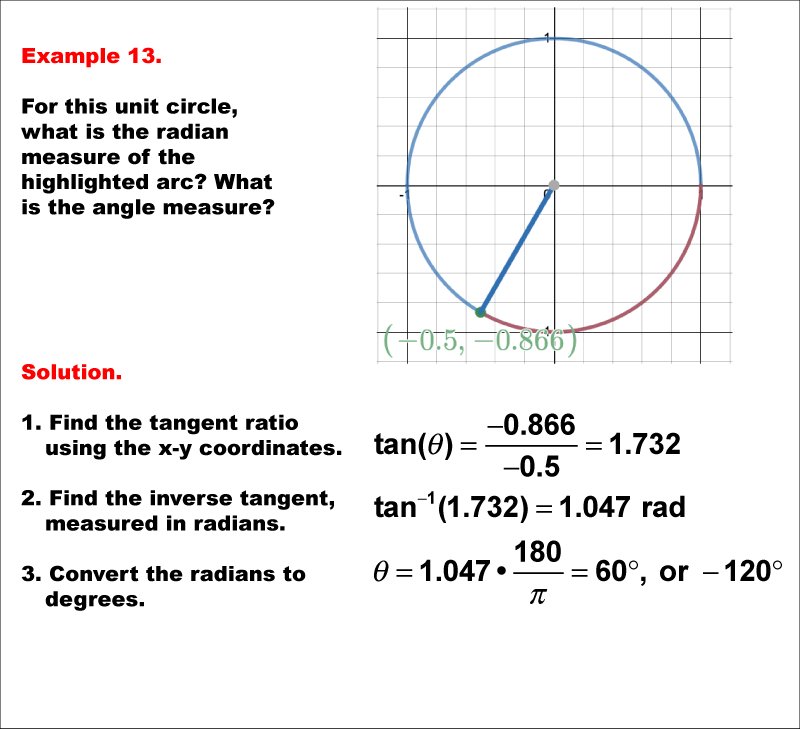
The image shows a unit circle with a point at (-0.5, -0.866), and the highlighted arc is in the third quadrant. The tangent ratio is calculated using these coordinates. The solution involves finding the inverse tangent and converting radians to degrees.
Example 13: The tangent ratio is calculated as tan(Θ) = -0.866 / -0.5 = 1.732. The inverse tangent is tan-1(1.732) = 1.047 radians. Converting this to degrees gives Θ = 60° or -120°.
These examples cover trigonometric ratios by demonstrating specific angles and calculations on the unit circle. Such visualizations aid in understanding the fundamental concepts of trigonometric functions.
By studying multiple worked-out examples, students gain deeper insight into the concept and can better recognize patterns in trigonometric functions.
Teacher's Script: Let's look at this example together. Notice how the angle is highlighted and how the tangent ratio is calculated. This visual can help you understand how trigonometric ratios work on a unit circle.
For a complete collection of math examples related to Trig Ratios click on this link: Math Examples: Trig Ratios and Radian Measures Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.SRT.C.6, CCSS.MATH.CONTENT.HSG.SRT.C.8, CCSS.MATH.CONTENT.HSF.TF.A.1, CCSS.MATH.CONTENT.HSF.TF.A.2, CCSS.MATH.CONTENT.HSF.TF.A.3, CCSS.MATH.CONTENT.HSF.TF.A.4 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Trig Expressions and Functions • Trigonometric Functions |
| Copyright Year | 2020 |
| Keywords | trig ratios, Unit Circle, radians |