Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 13
Topic
Geometry
Description
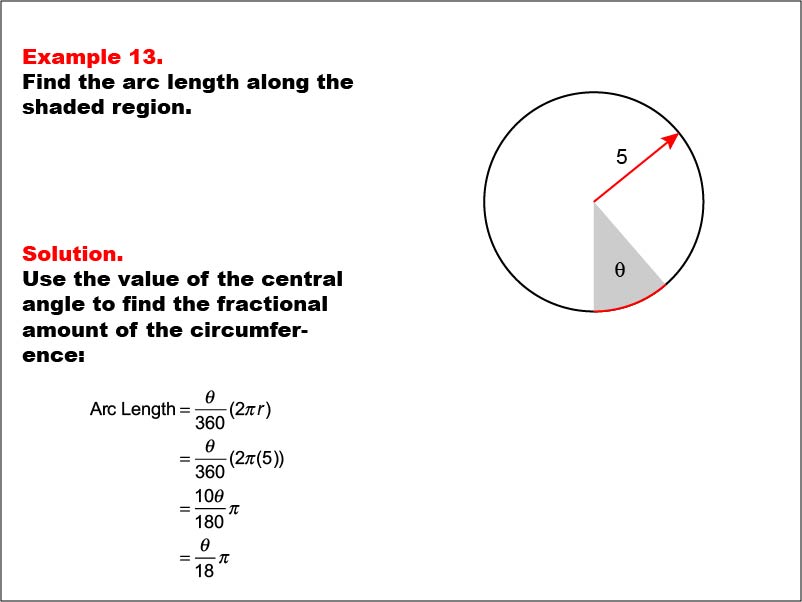
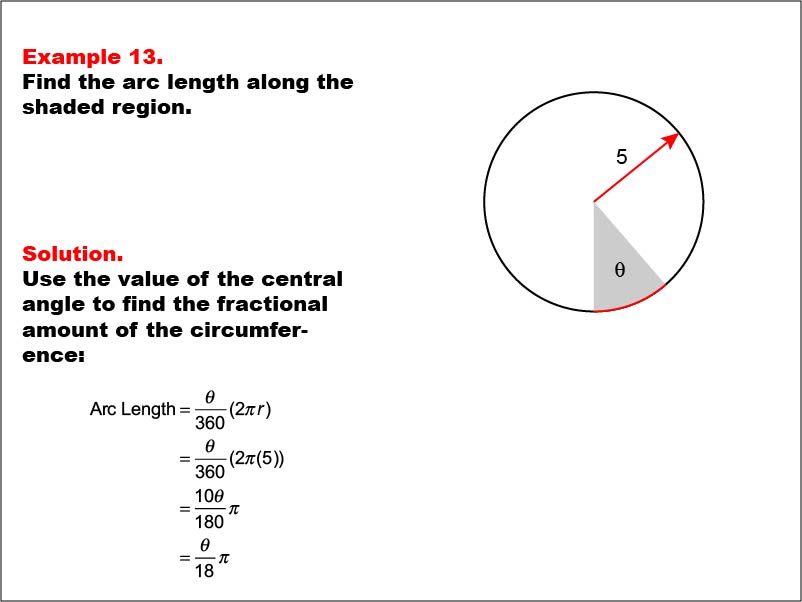
This example presents a circle with a radius of 5 units and a shaded sector with central angle θ (theta). The task is to express the arc length of the shaded region in terms of θ. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (θ / 360) * (2 * π * 5) = θ / 18 * π.
Understanding arc length calculations with variable angles helps students develop a more flexible approach to circular geometry. This example builds upon previous concepts while challenging students to work with a combination of fixed and variable measurements.
Exposure to problems that involve both constants and variables prepares students for more advanced mathematical thinking. These examples foster the development of algebraic reasoning skills within a geometric context, bridging the gap between different areas of mathematics.
Teacher: "Let's explore how the variable θ affects our calculation. How does the final expression θ / 18 * π change as θ increases or decreases? Can you think of a real-world situation where you might need to calculate an arc length with a known radius but unknown angle?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |