Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 17
Topic
Geometry
Description
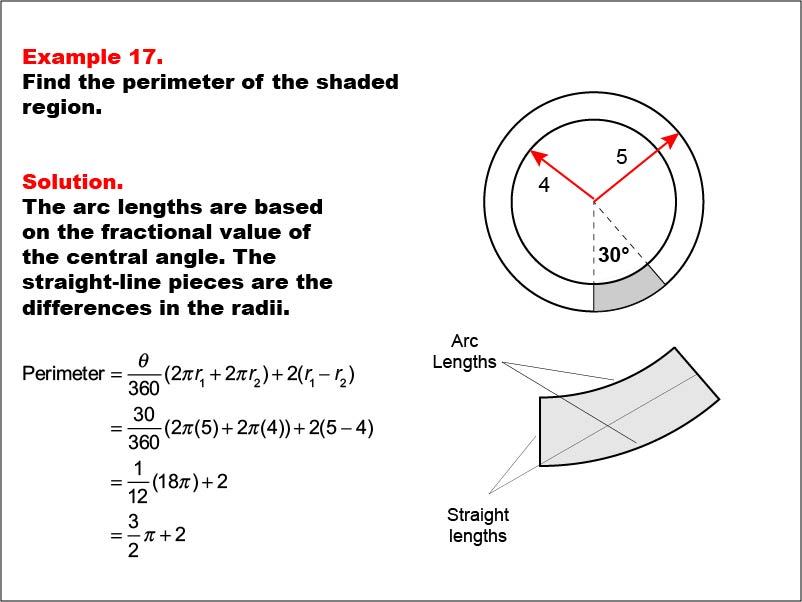
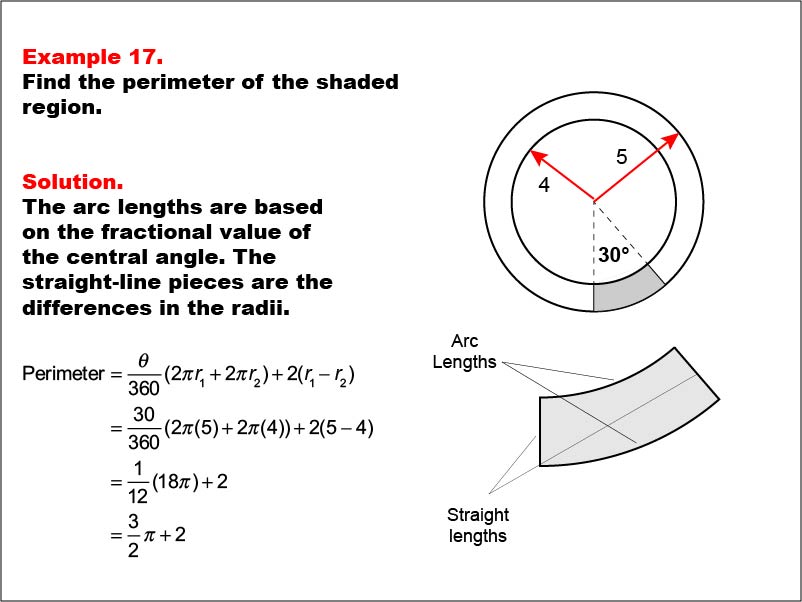
This example presents two concentric circles with radii of 5 and 4 units, and a shaded sector with a central angle of 30 degrees. The task is to calculate the perimeter of the shaded region. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * r1 + 2 * π * r2) + 2 * (r1 - r2) = (30 / 360) * (2π * 5 + 2π * 4) + 2 * (5 - 4) = 3π / 2 + 2.
Calculating perimeters of complex shapes like sectors between concentric circles helps students develop problem-solving skills and spatial reasoning. This example combines concepts of arc length and linear distance, encouraging a more holistic understanding of geometric measurements.
Exposure to multi-step problems that involve both circular and linear elements prepares students for more advanced mathematical thinking. These examples foster the development of analytical skills within a geometric context, bridging the gap between different areas of mathematics.
Teacher: "Consider why we need to include both arc lengths and straight-line segments in this calculation. How does the central angle affect each part of the perimeter? Can you think of a real-world situation where calculating such a perimeter might be useful?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |