Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 22
Topic
Geometry
Description
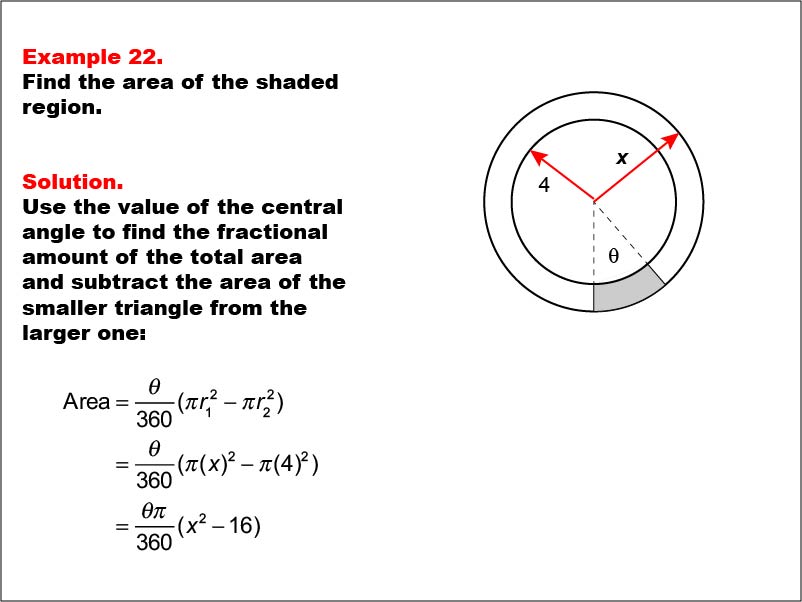
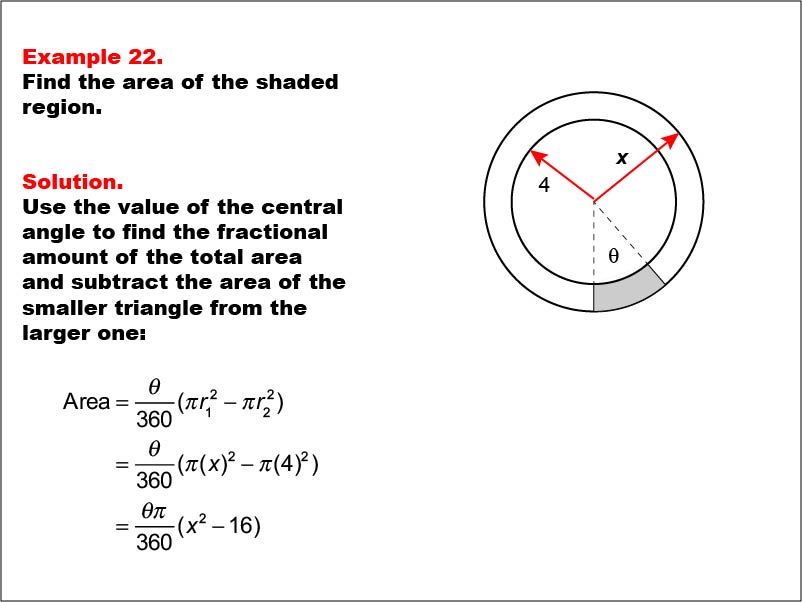
This example presents two concentric circles with radii 4 and x, and a shaded sector with a central angle θ (theta). The task is to express the area of the shaded region in terms of x and θ. The solution uses the central angle to find the fractional area difference between the larger and smaller circles: Area = (θ / 360) * (π * x2 - π * 42) = (θ * π / 360) * (x2 - 16).
Working with variable expressions in geometric problems enhances students' algebraic thinking and prepares them for more advanced mathematical concepts. This example demonstrates how to generalize the solution for concentric circles with one known and one unknown radius, fostering a deeper understanding of the relationships between variables in geometric formulas.
Presenting examples that combine specific values with variables helps students transition from concrete to abstract thinking. This approach is crucial for building a strong foundation in mathematics and preparing for higher-level courses.
Teacher: "Consider how the variables x and θ affect our calculation. How does the final expression change as each variable increases or decreases? Can you interpret what x2 - 16 represents geometrically in this context?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |