Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 23
Topic
Geometry
Description
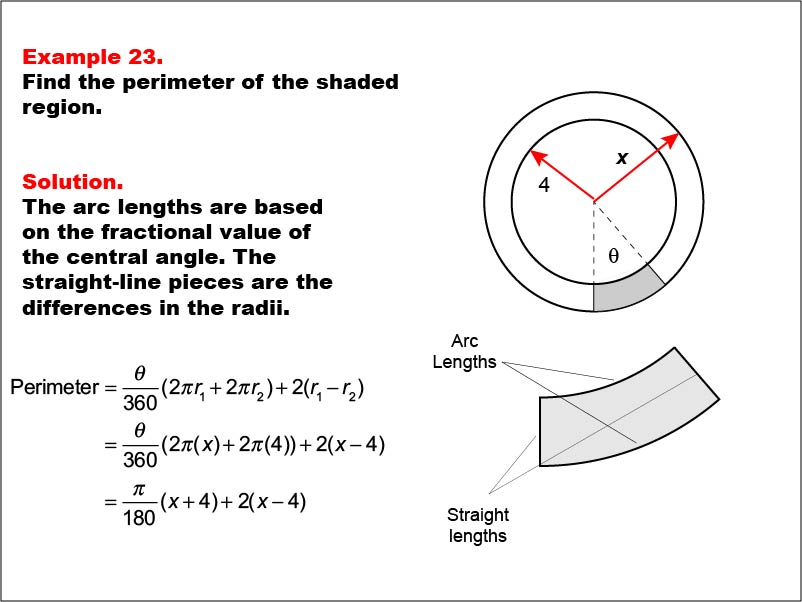
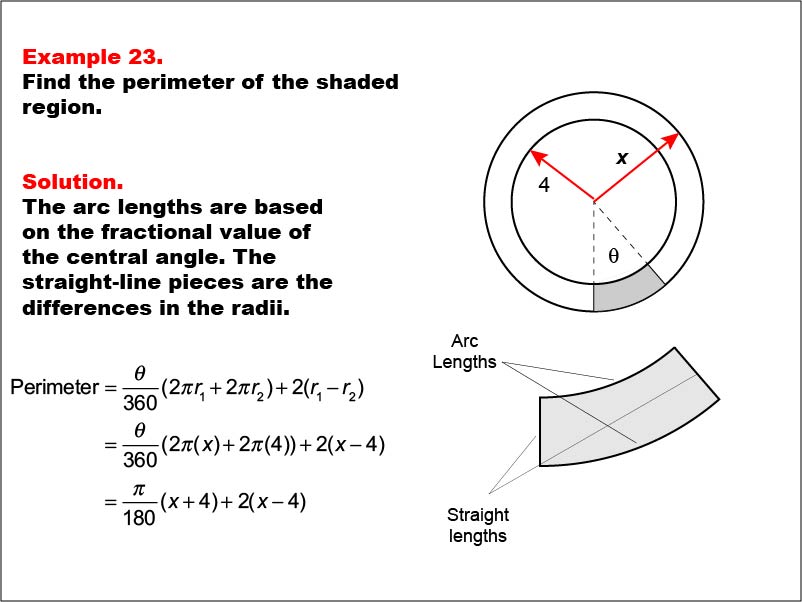
This example features two concentric circles with radii x and 4, and a shaded sector with a central angle θ (theta). The task is to express the perimeter of the shaded region in terms of x and θ. The solution involves calculating arc lengths based on the central angle and adding straight-line segments between radii: Perimeter = (θ / 360) * (2 * π * x + 2 * π * 4) + 2 * (x - 4) = (π / 180) * θ(x + 4) + 2(x - 4).
Calculating perimeters of complex shapes with both known and unknown dimensions helps students develop advanced problem-solving skills and spatial reasoning. This example combines concepts of arc length and linear distance with algebraic expressions, encouraging a more sophisticated understanding of geometric measurements.
Exposure to multi-step problems that involve both circular and linear elements, as well as multiple variables, prepares students for more advanced mathematical thinking. These examples foster the development of analytical and algebraic skills within a geometric context, bridging the gap between different areas of mathematics.
Teacher: "Let's break down each part of this formula. How do the variables x and θ affect different aspects of the perimeter? Can you explain why we add (x + 4) in one part of the formula but subtract (x - 4) in another? How would the perimeter change if we increased θ while keeping x constant?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |