Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 8
Topic
Geometry
Description
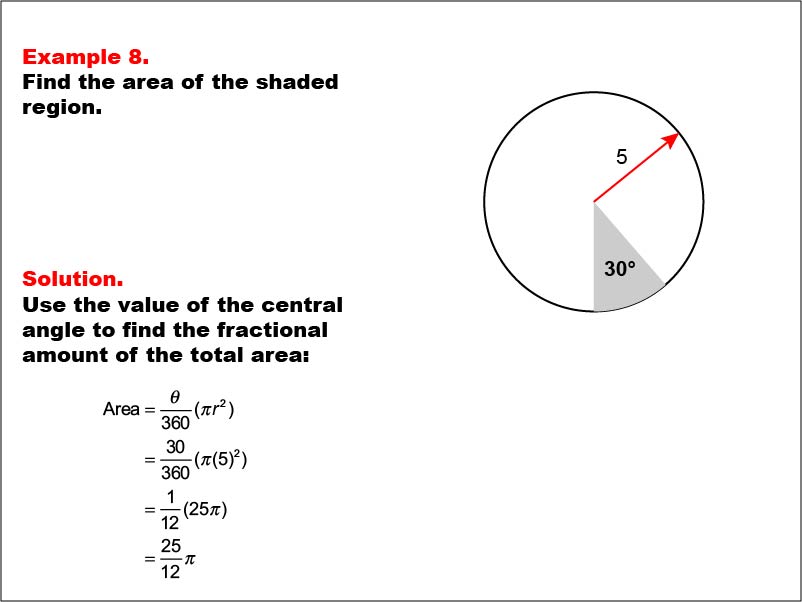
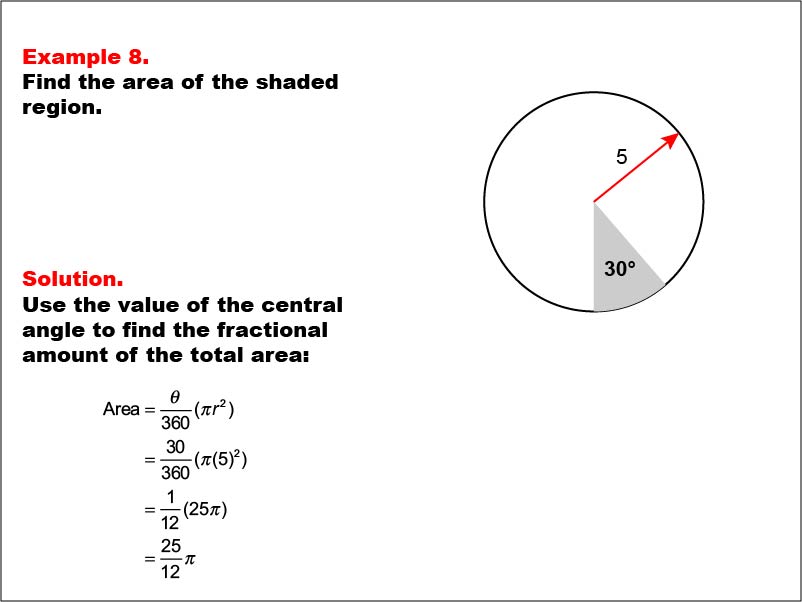
This example presents a circle with a radius of 5 units and a shaded sector with a central angle of 30 degrees. The task is to calculate the area of the shaded sector. The solution involves using the central angle to find the fractional amount of the total area: A = (30 / 360) * π * 52 = 25π / 12.
Understanding sectors of circles introduces students to the concept of proportional reasoning in geometry. This example demonstrates how the central angle relates to the fraction of the circle's area, bridging the gap between angle measurements and area calculations.
Exposure to various types of circular problems, including sectors, helps students develop a comprehensive understanding of circular geometry. These examples prepare students for more complex problems involving arcs, sectors, and segments of circles, which are essential in many real-world applications.
Teacher: "Let's think about why we use the fraction 30/360 in this calculation. How does this relate to the concept of a full circle? Can you predict how the area would change if we doubled the central angle?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |