Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9
Display Title
Math Example--Area and Perimeter--Circular Area and Circumference: Example 9
Topic
Geometry
Description
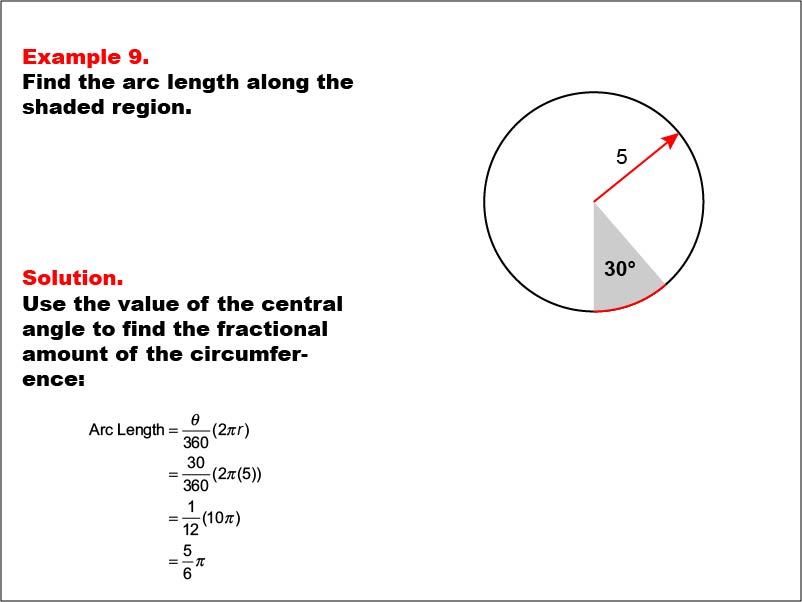
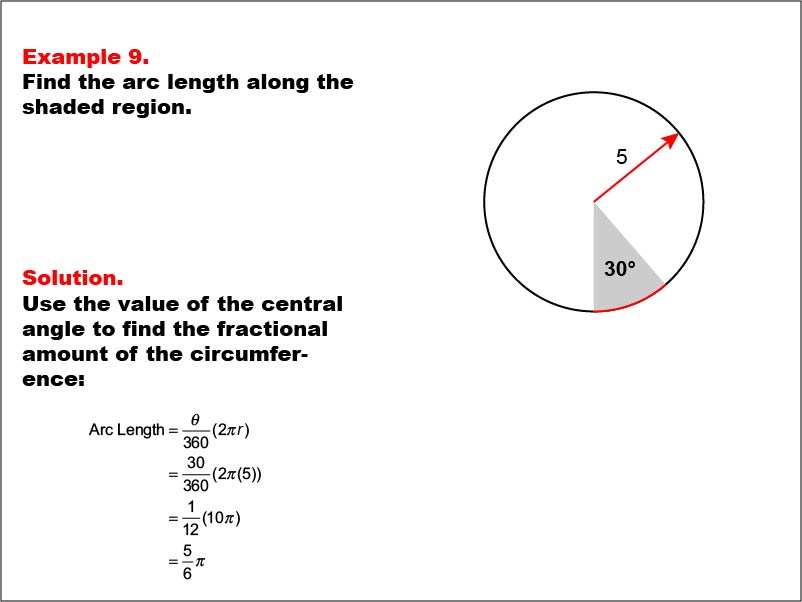
This example features a circle with a radius of 5 units and a shaded arc corresponding to a central angle of 30 degrees. The task is to calculate the length of the shaded arc. The solution involves using the central angle to find the fractional amount of the circumference: Arc Length = (30 / 360) * 2 * π * 5 = 5π / 6.
Understanding arc length calculations is crucial for students to grasp the relationship between central angles and portions of a circle's circumference. This example builds upon previous concepts of circumference while introducing the idea of partial circular measurements.
Presenting multiple examples that explore different aspects of circular geometry helps students develop a comprehensive understanding of these concepts. By working through various problem types, students learn to apply formulas flexibly and interpret results in different contexts.
Teacher: "Consider how this calculation relates to finding the full circumference. How does the fraction 30/360 represent the portion of the circle we're interested in? Can you think of a real-world situation where calculating arc length might be useful?"
For a complete collection of math examples related to Circular Area and Circumference click on this link: Math Examples: Circular Area and Circumference Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Circles • Area and Circumference |
| Copyright Year | 2013 |
| Keywords | area, circumference, circle |