Display Title
Math Example--Area and Perimeter--Surface Area: Example 18
Display Title
Math Example--Area and Perimeter--Surface Area: Example 18
Topic
Surface Area
Description
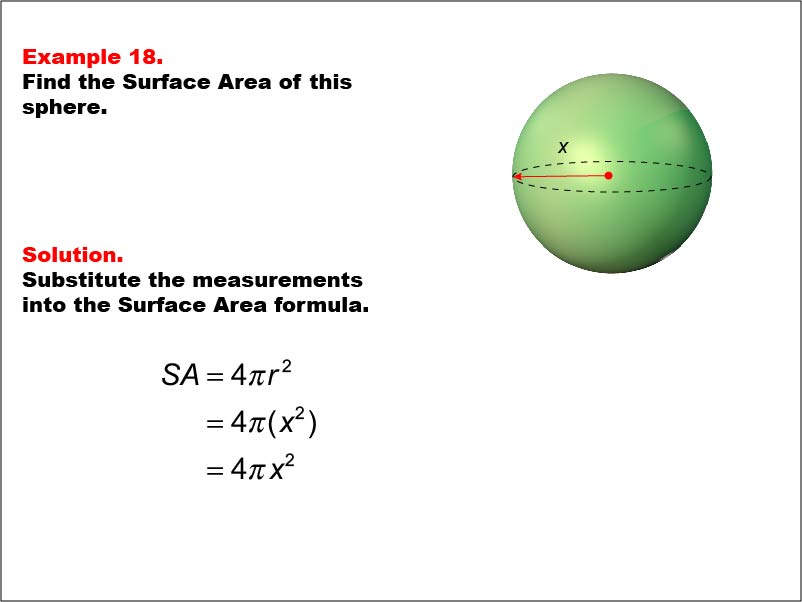
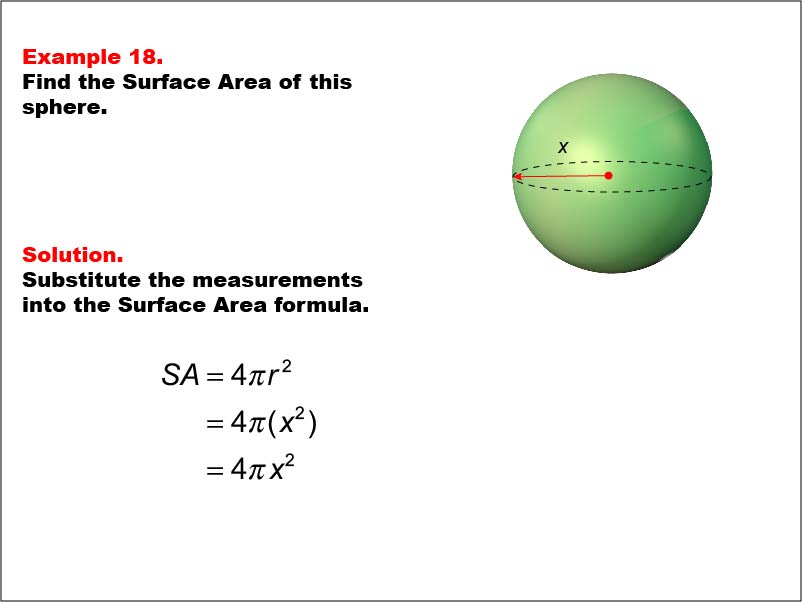
This example presents a general formula for calculating the surface area of a sphere with an unknown radius labeled as "x". The surface area is calculated using the formula SA = 4πr2, which in this case becomes SA = 4πx2, where x is the radius of the sphere.
Understanding surface area calculations for three-dimensional curved shapes with variable dimensions is crucial in advanced mathematics and its applications. This collection of examples helps teach the topic by presenting progressively challenging scenarios, allowing students to apply and extend their knowledge of basic surface area principles to more sophisticated problems with general formulas for curved surfaces.
Engaging with multiple worked-out examples is essential for students to fully comprehend advanced surface area calculations with variables, especially for curved shapes like spheres. Each example builds upon previous concepts while introducing new complexities, helping students develop critical thinking skills and the ability to approach novel geometric problems with confidence and flexibility, particularly when dealing with curved surfaces and variable dimensions.
Teacher's Script: In this example, we're exploring a generalized formula for the surface area of a sphere. Notice how we use the variable 'x' to represent the radius, making our formula applicable to spheres of any size. As we work through this, think about how this general approach relates to the specific sphere example we saw earlier. This type of thinking will be invaluable as you encounter more complex geometric problems involving curved surfaces and variables in your future studies and real-world applications.
For a complete collection of math examples related to Surface Area click on this link: Math Examples: Surface Area Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.6 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Surface Area and Volume • Surface Area |
| Copyright Year | 2013 |
| Keywords | surface area |