Display Title
Math Example--Area and Perimeter--Surface Area: Example 5
Display Title
Math Example--Area and Perimeter--Surface Area: Example 5
Topic
Surface Area
Description
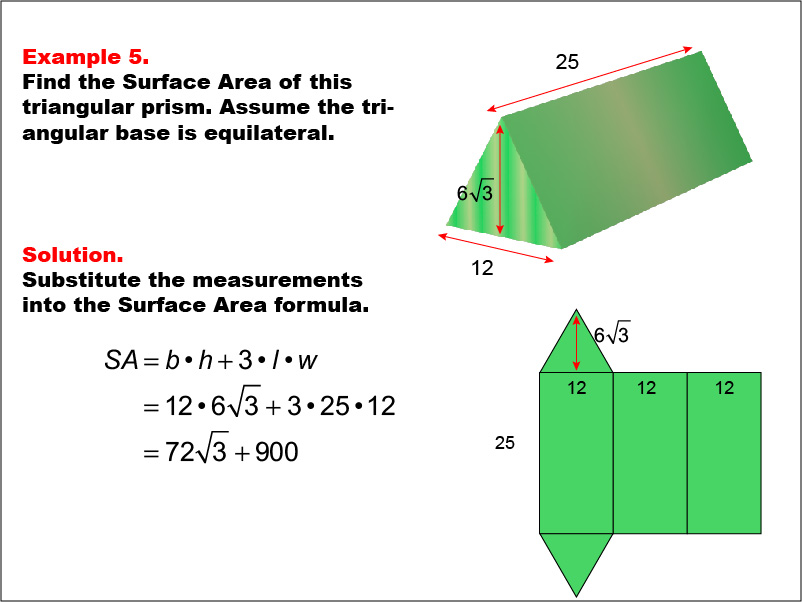
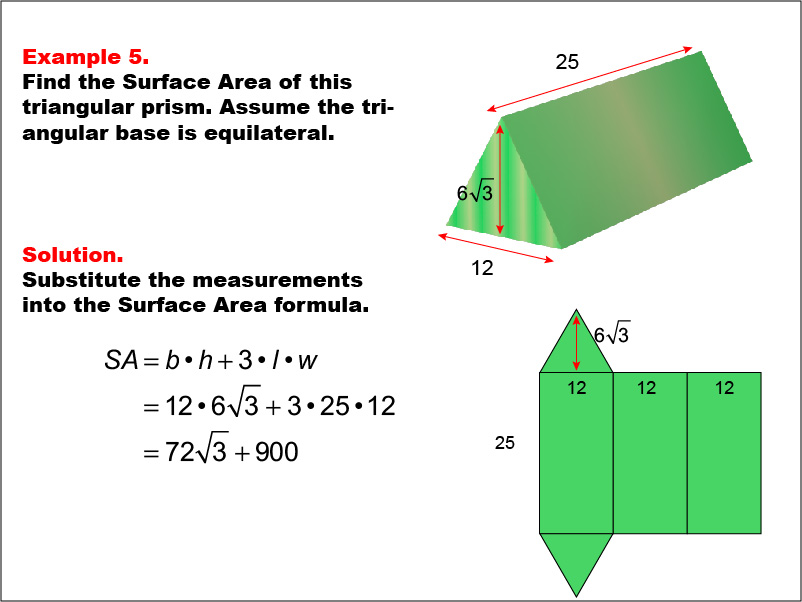
This example demonstrates the calculation of surface area for a triangular prism with an equilateral triangular base. The base is 12 units, the height is 6 * √(3), and the length of the prism is 25 units. The surface area is calculated using the formula SA = b * h + 3 * l * w, where b is the base, h is the height of the triangle, l is the length of the prism, and w is the width of the triangle. The final result is 72 * √(3) + 900 square units.
Understanding surface area calculations for various geometric shapes is essential in mathematics and its applications. This collection of examples helps teach the topic by introducing different types of prisms, allowing students to apply surface area principles to more diverse shapes and reinforce their understanding of geometric relationships.
Exposure to multiple worked-out examples is crucial for students to fully grasp the concept of surface area across different shapes. Each example builds upon previous knowledge while introducing new geometric forms, helping students develop versatility in their problem-solving approach and a deeper understanding of spatial relationships.
Teacher's Script: Today, we're exploring the surface area of a triangular prism. Notice how we break down the calculation into the area of the triangular bases and the rectangular sides. As we work through this example, think about how this approach compares to our previous calculations with rectangular prisms. Understanding these similarities and differences will help you tackle surface area problems for various shapes in the future.
For a complete collection of math examples related to Surface Area click on this link: Math Examples: Surface Area Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.6 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Surface Area and Volume • Surface Area |
| Copyright Year | 2013 |
| Keywords | surface area |