Display Title
Math Example--Area and Perimeter--Surface Area: Example 9
Display Title
Math Example--Area and Perimeter--Surface Area: Example 9
Topic
Surface Area
Description
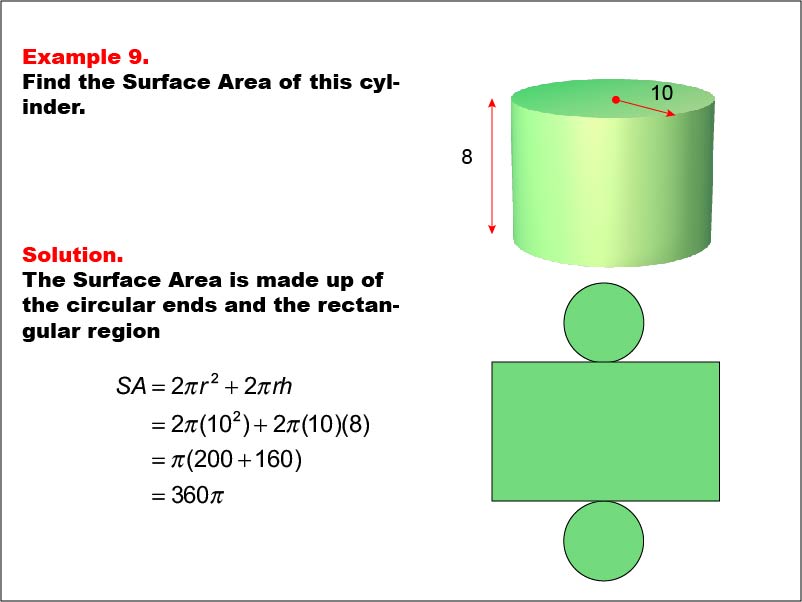
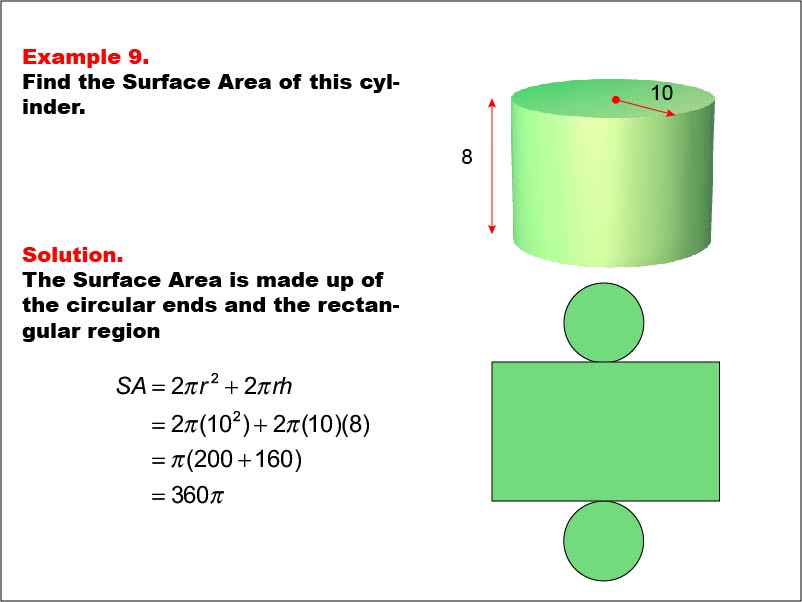
This example demonstrates the calculation of surface area for a cylinder with a radius of 10 units and a height of 8 units. The surface area consists of two circular ends and the rectangular region forming the curved surface. The formula used is SA = 2πr2 + 2πrh, where r is the radius and h is the height. For this specific cylinder, the calculation yields a surface area of 360π square units.
Understanding surface area calculations for three-dimensional curved shapes like cylinders is essential in mathematics and its applications. This collection of examples helps teach the topic by introducing different types of solids, allowing students to apply surface area principles to more diverse shapes and reinforce their understanding of geometric relationships.
Engaging with multiple worked-out examples is crucial for students to fully grasp the concept of surface area across different shapes. Each example builds upon previous knowledge while introducing new geometric forms, helping students develop versatility in their problem-solving approach and a deeper understanding of spatial relationships, especially when dealing with curved surfaces.
Teacher's Script: Today, we're exploring the surface area of a cylinder. Notice how we break down the calculation into the areas of the circular ends and the rectangular region that forms the curved surface. As we work through this example, think about how this approach compares to our previous calculations with prisms. Understanding these similarities and differences will help you tackle surface area problems for various shapes, including those with curved surfaces, in the future.
For a complete collection of math examples related to Surface Area click on this link: Math Examples: Surface Area Collection.
| Common Core Standards | CCSS.MATH.CONTENT.7.G.B.6 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Surface Area and Volume • Surface Area |
| Copyright Year | 2013 |
| Keywords | surface area |