Display Title
Math Example--Complex Numbers--Complex Coordinates--Example 5
Display Title
Math Example--Complex Numbers--Complex Coordinates--Example 5
Topic
Complex Numbers
Description
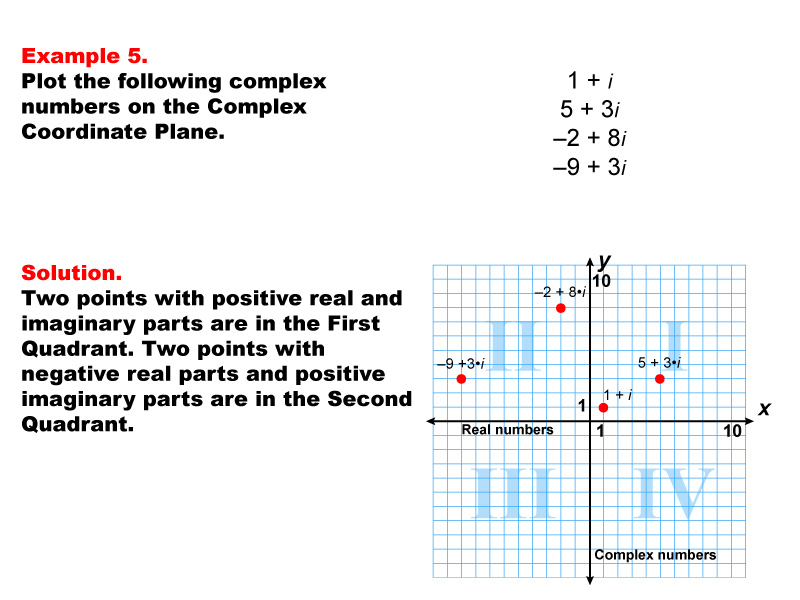
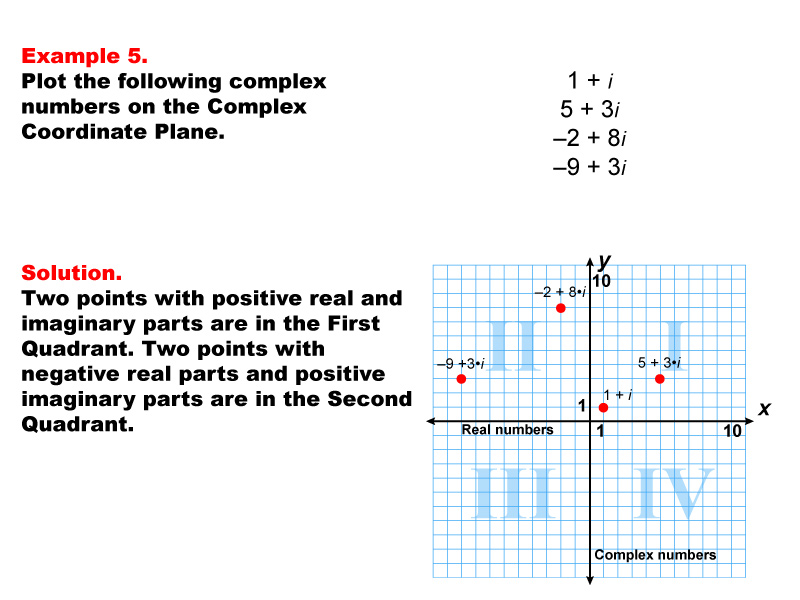
This image presents Example 5 of a series on complex numbers, showcasing how to plot specific complex numbers on the complex coordinate plane. The complex numbers given are: 1 + i, 5 + 3i, -2 + 8i, and -9 + 3i. Example 5. Plot the following complex numbers on the Complex Coordinate Plane: 1 + i, 5 + 3i, -2 + 8i, -9 + 3i. Solution: Two points with positive real and imaginary parts are in the First Quadrant. Two points with negative real parts and positive imaginary parts are in the Second Quadrant.
Complex numbers allow for a two-dimensional representation of numbers using real and imaginary components. Examples like these help students grasp how to plot complex coordinates, understanding both real and imaginary axes.
Seeing multiple worked-out examples is crucial for students to fully understand complex concepts like plotting complex numbers. Through varied examples, students can see consistent patterns and learn effective strategies.
Teacher’s Script: Imagine a number line that moves in two directions. Each complex number has a place on this plane, just like how we plot coordinates. Let's use this example to practice reading and plotting complex coordinates.
For a complete collection of math examples related to Complex Numbers click on this link: Math Examples: Complex Coordinates Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.B.4, CCSS.MATH.CONTENT.HSN.CN.B.5, CCSS.MATH.CONTENT.HSN.CN.B.6 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Numerical and Algebraic Expressions |
| Copyright Year | 2020 |
| Keywords | complex numbers |