Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 22
Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 22
Topic
Geometry
Description
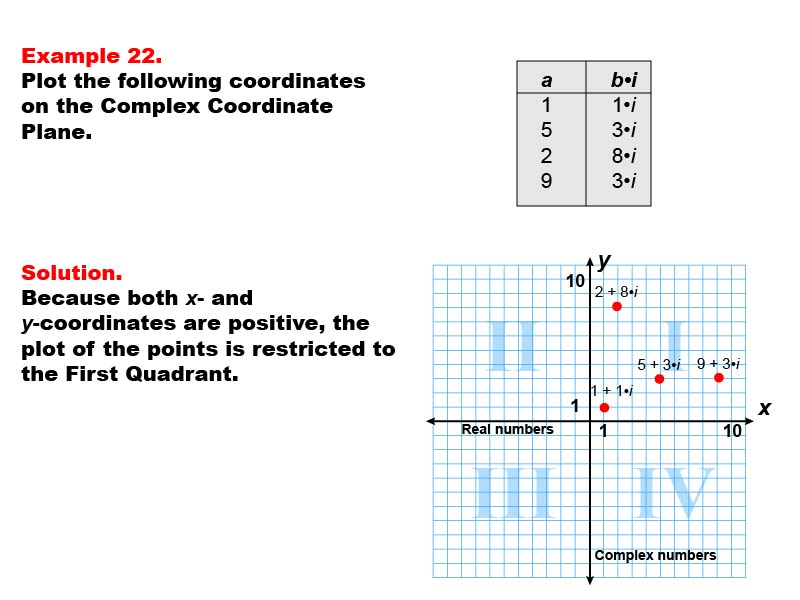
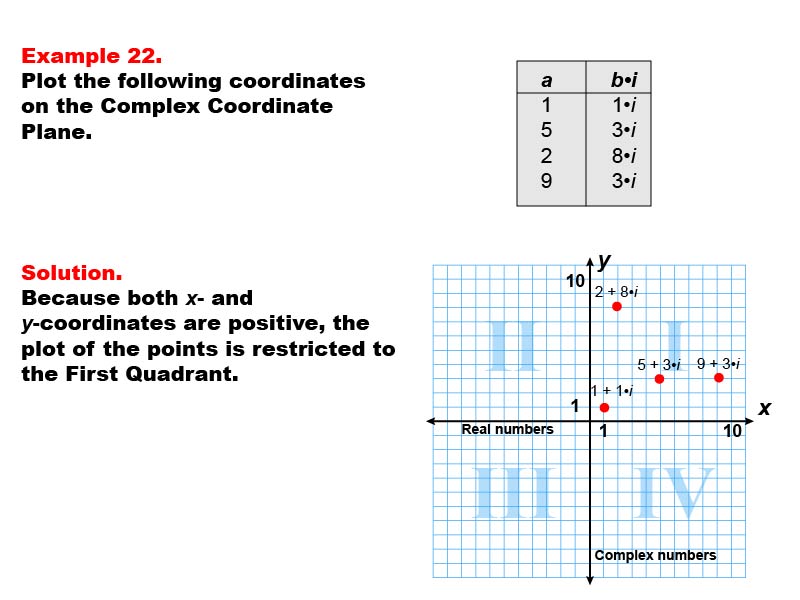
This example introduces the concept of complex numbers on a coordinate plane. The image illustrates a complex coordinate plane with four points plotted in the first quadrant: 1 + 1i, 5 + 3i, 2 + 8i, and 9 + 3i. These points represent complex numbers with positive real and imaginary parts.
Understanding complex numbers and their representation on a coordinate plane is crucial in advanced mathematics and various scientific fields. This example helps students visualize how complex numbers are plotted, with the real part on the x-axis and the imaginary part on the y-axis.
By providing multiple examples of complex numbers in the first quadrant, students can develop a clear understanding of how complex numbers relate to the Cartesian coordinate system they are already familiar with.
Teacher's Script: Take a close look at how these complex numbers are plotted. Notice that the real part determines the x-coordinate, while the imaginary part determines the y-coordinate. Can you explain why all these points are in the first quadrant? Let's discuss how this representation of complex numbers extends our understanding of the coordinate plane.
For a complete collection of math examples related to Coordinate Systems click on this link: Math Examples: Coordinate Systems Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.NS.C.8 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • Coordinate Systems |
| Copyright Year | 2013 |
| Keywords | coordinate geometry, coordinate system, coordinate systems |