Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 24
Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 24
Topic
Geometry
Description
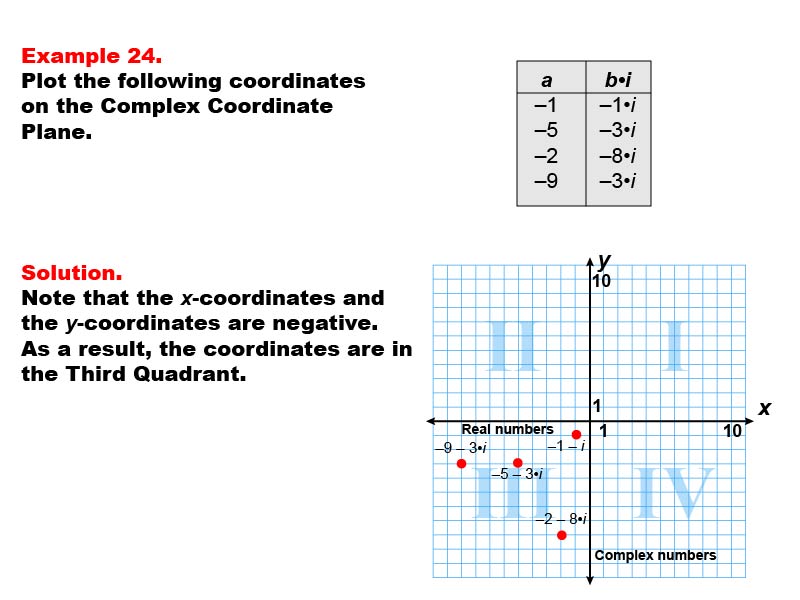
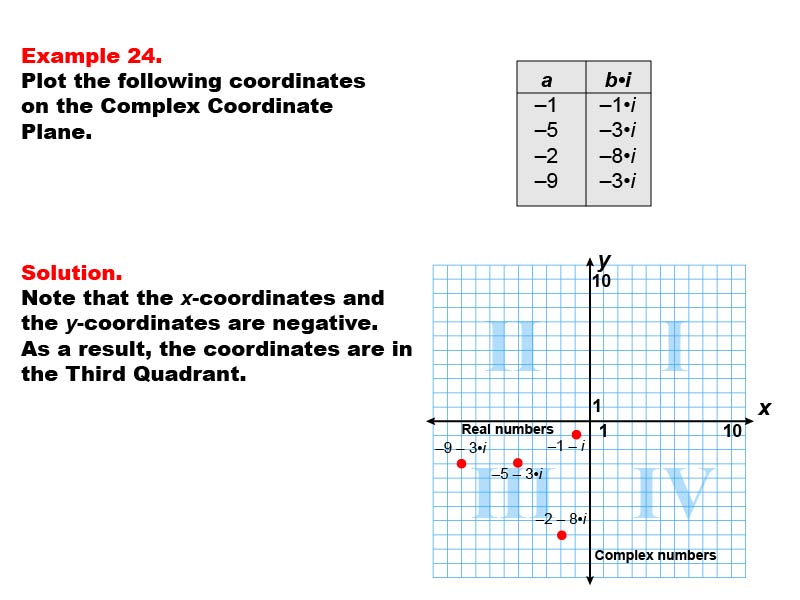
This example demonstrates plotting complex numbers in the third quadrant of the complex plane. The image displays four points: -1 - 1i, -5 - 3i, -2 - 8i, and -9 - 3i. These points represent complex numbers with both negative real and imaginary parts.
Understanding how to plot complex numbers in all quadrants is crucial for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with negative real and imaginary parts are positioned on the complex plane.
By providing multiple examples of complex numbers in the third quadrant, students can develop a deeper understanding of the relationship between complex numbers and their geometric representation.
Teacher's Script: Examine how these complex numbers are plotted in the third quadrant. Notice that both the real and imaginary parts are negative, placing the points to the left of the y-axis and below the x-axis. Can you explain why these points are specifically in the third quadrant? Let's discuss how this relates to our understanding of both complex numbers and coordinate geometry.
For a complete collection of math examples related to Coordinate Systems click on this link: Math Examples: Coordinate Systems Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.NS.C.8 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • Coordinate Systems |
| Copyright Year | 2013 |
| Keywords | coordinate geometry, coordinate system, coordinate systems |