Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 32
Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 32
Topic
Geometry
Description
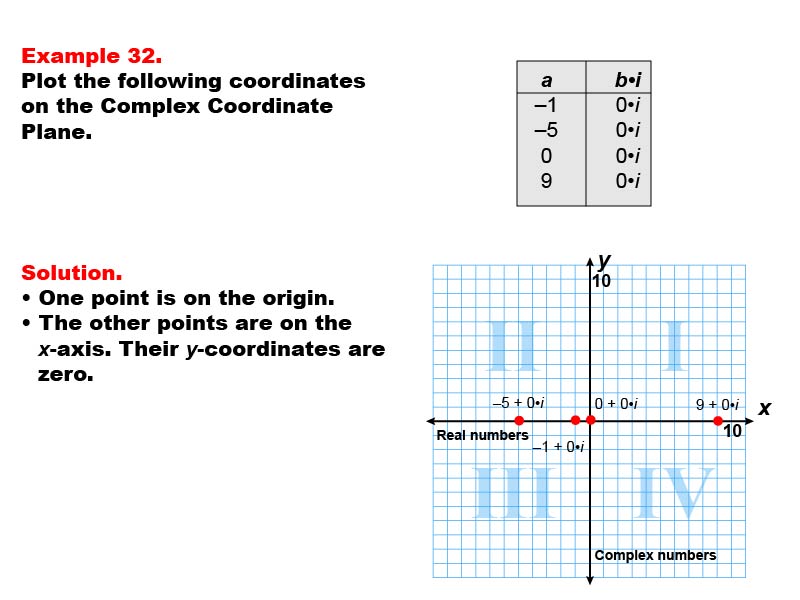
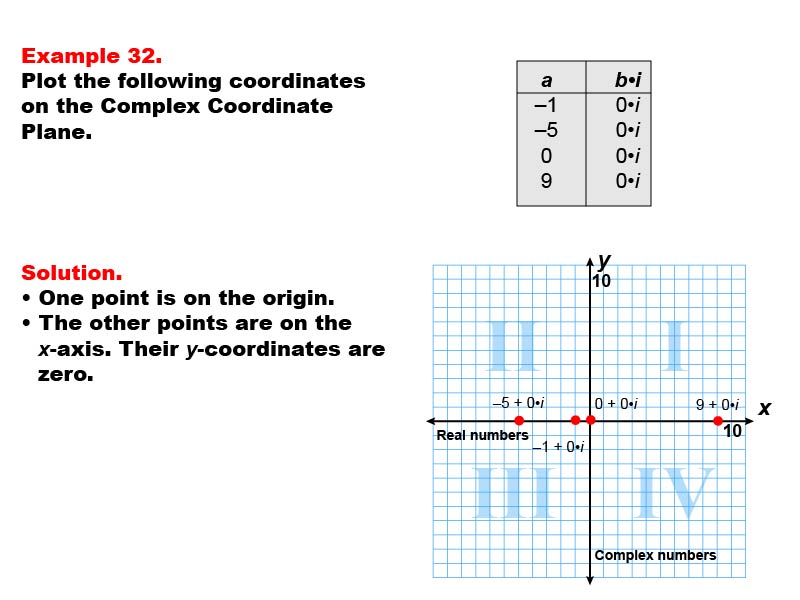
This example demonstrates plotting points on the real axis of the complex plane. The image shows four points: (-5, 0), (-1, 0), (0, 0), and (9, 0). These points represent real numbers on the complex plane, where the imaginary part is zero.
Understanding how to plot real numbers on the complex plane is crucial for developing a comprehensive grasp of complex number theory. This example helps students visualize that real numbers are a subset of complex numbers, lying on the real axis of the complex plane.
By providing examples of points on the real axis, including positive and negative numbers and zero, students can develop a deeper understanding of the relationship between real numbers and their representation on the complex plane. This approach reinforces the concept that real numbers are complex numbers with a zero imaginary part.
Teacher's Script: Observe how these points are plotted on the real axis of the complex plane. Notice that all points have a y-coordinate (imaginary part) of zero. Can you explain why these points represent real numbers? Let's discuss the significance of the real axis in the complex plane and how it relates to our understanding of real and complex numbers.
For a complete collection of math examples related to Coordinate Systems click on this link: Math Examples: Coordinate Systems Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.NS.C.8 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • Coordinate Systems |
| Copyright Year | 2013 |
| Keywords | coordinate geometry, coordinate system, coordinate systems |