Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 9
Display Title
Math Example--Coordinate Geometry--Coordinate Systems: Example 9
Topic
Geometry
Description
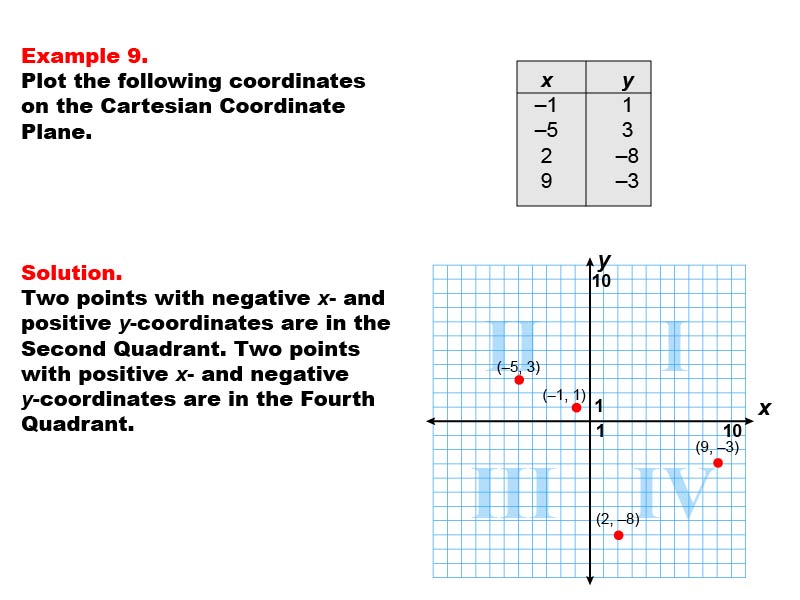
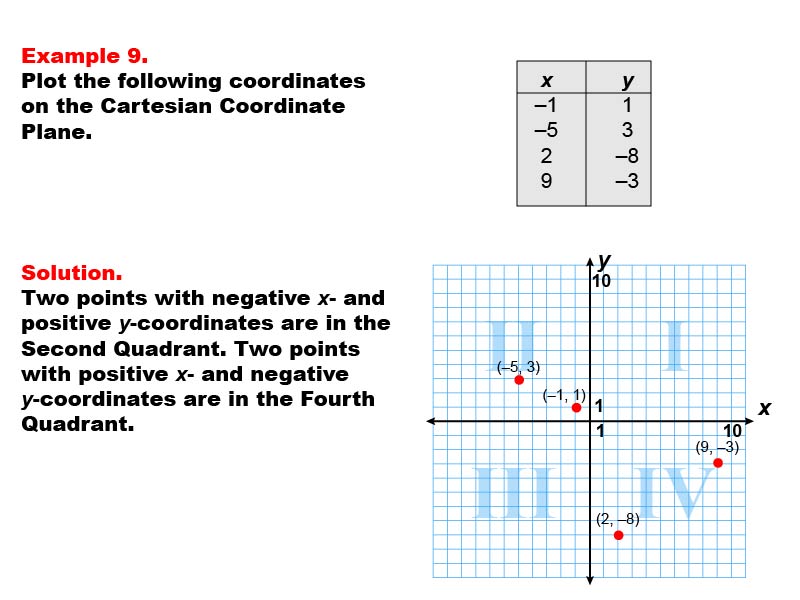
This example showcases plotting coordinates in both the second and fourth quadrants of the Cartesian Coordinate Plane. The image displays four points: (-1, 1) and (-5, 3) in the second quadrant, and (2, -8) and (9, -3) in the fourth quadrant. This example demonstrates how points can be distributed across quadrants that are diagonally opposite to each other.
Understanding how to plot points across multiple quadrants, especially those diagonally opposite, is crucial for developing a comprehensive grasp of coordinate geometry. This collection of examples helps students visualize the relationship between coordinate pairs and their positions on the plane, particularly when dealing with points that have opposite signs for both coordinates.
By providing examples that span diagonally opposite quadrants, students can develop a more nuanced understanding of the Cartesian coordinate system. This approach helps reinforce the concept of how the signs of x and y coordinates determine a point's quadrant and the relationship between diagonally opposite quadrants.
Teacher's Script: Take note of how the signs of the coordinates determine which quadrant each point is in. The points with negative x and positive y are in the second quadrant, while those with positive x and negative y are in the fourth quadrant. Can you explain the relationship between these diagonally opposite quadrants? If you're interested in exploring this concept further, let's discuss how changing the signs of both coordinates affects a point's position.
For a complete collection of math examples related to Coordinate Systems click on this link: Math Examples: Coordinate Systems Collection.
| Common Core Standards | CCSS.MATH.CONTENT.6.NS.C.8 |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • Coordinate Systems |
| Copyright Year | 2013 |
| Keywords | coordinate geometry, coordinate system, coordinate systems |