Display Title
Math Example--Coordinate Geometry--Distance Formula: Example 14
Display Title
Math Example--Coordinate Geometry--Distance Formula: Example 14
Topic
Geometry
Description
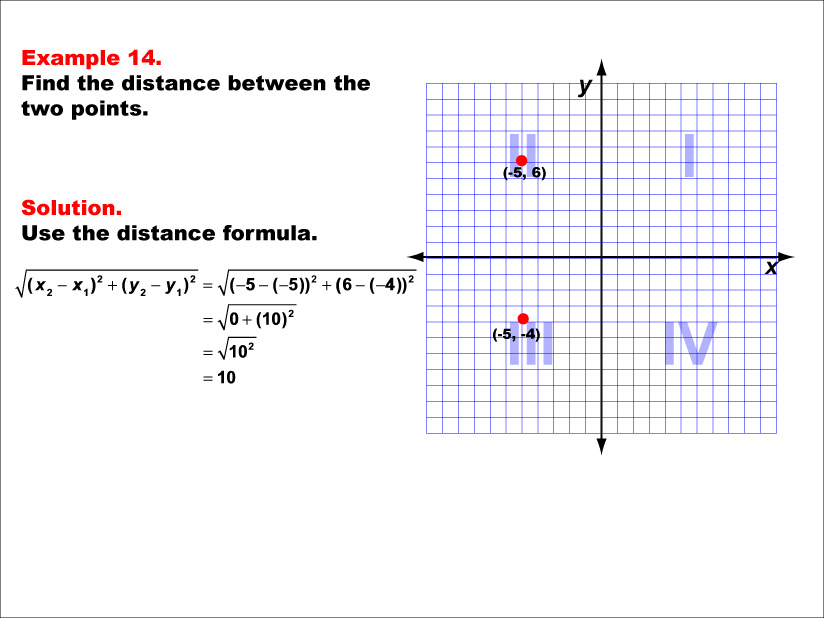
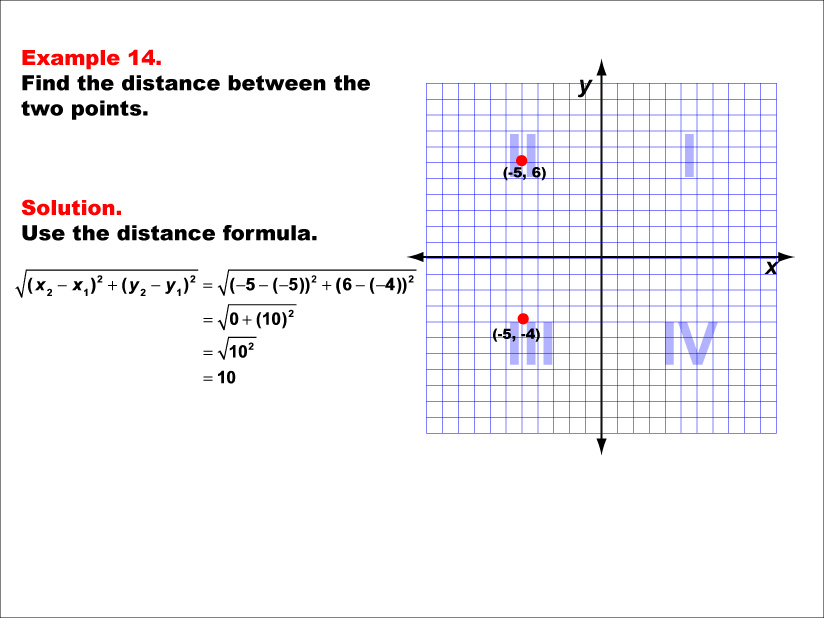
This example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (-5, 6) and (-5, -4) are plotted on a graph, and the distance between them is determined using the formula: √((-5 - (-5))2 + (6 - (-4))2) = √(0 + 102) = 10.
The distance formula is a key concept in coordinate geometry, allowing students to find the length of a line segment given the coordinates of its endpoints. This collection of examples showcases various applications of the formula, helping students understand its versatility in solving geometric problems across different scenarios, including vertical distances and points with negative coordinates.
Providing multiple worked-out examples is essential for students to fully comprehend the distance formula and its applications. By observing the formula in action across different contexts, students can develop a more robust understanding of how to apply it effectively. This approach also reinforces the step-by-step process of using the formula, enabling students to tackle similar problems with confidence.
Teacher Script: "In this fourteenth example, we're working with the points (-5, 6) and (-5, -4). Notice how these points have the same x-coordinate, creating a vertical line. As we apply the distance formula, pay attention to how this affects our calculation. What happens to the first term under the square root? How does this simplify our calculation, and why is our final answer a whole number?"
For a complete collection of math examples related to Geometry click on this link: Math Examples: Distance Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.G.B.8, CCSS.MATH.CONTENT.HSG.GPE.B.4, CCSS.MATH.CONTENT.HSG.GPE.B.7 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • The Distance Formula |
| Copyright Year | 2013 |
| Keywords | pythagorean theorem, coordinate, square root, radical, distance formula |