Display Title
Math Example--Coordinate Geometry--The Midpoint Formula: Example 17
Display Title
Math Example--Coordinate Geometry--The Midpoint Formula: Example 17
Topic
Coordinate Geometry
Description
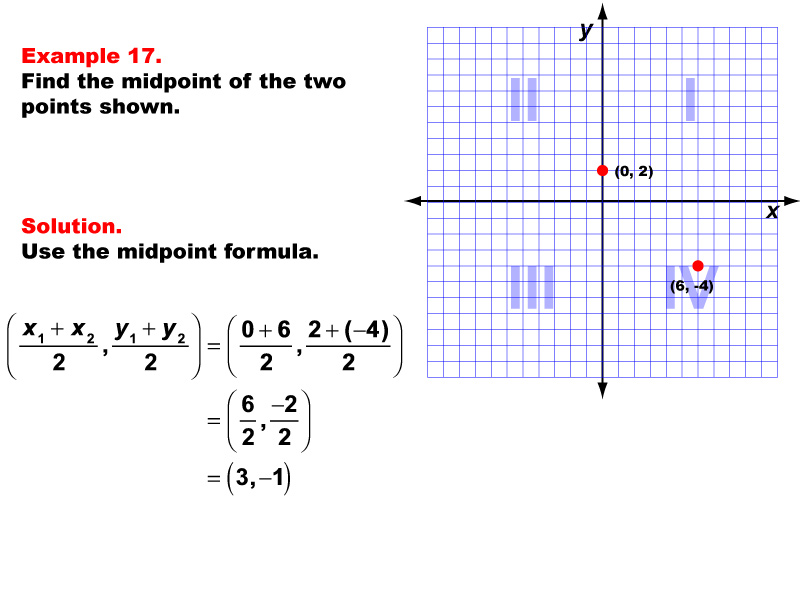
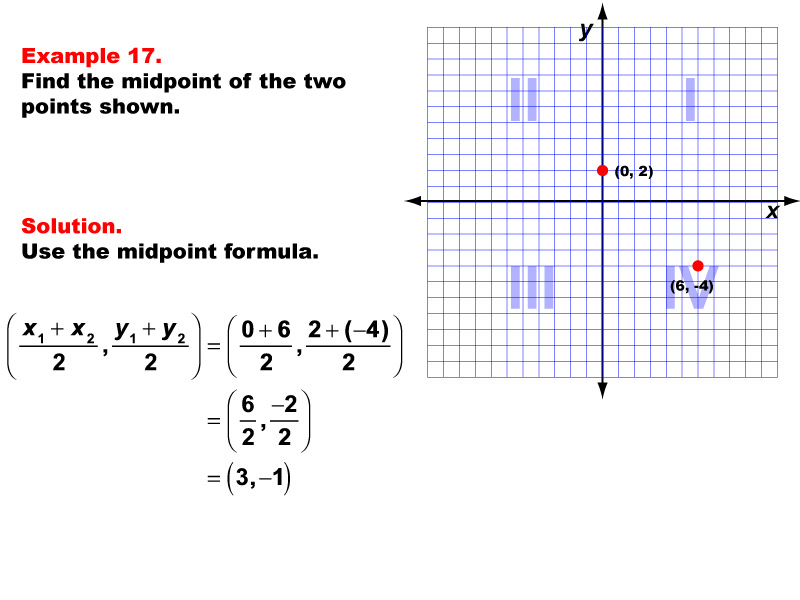
This example illustrates the application of the midpoint formula to find the center point between (0, 2) and (6, -4) on a coordinate plane. Using the formula ( ( x1 + x2 ) / 2, ( y1 + y2 ) / 2 ), we substitute the given values: ( ( 0 + 6 ) / 2, ( 2 + (-4) ) / 2 ) = ( 6 / 2, -2 / 2 ) = ( 3, -1 ). The resulting midpoint is (3, -1).
The midpoint formula is a fundamental concept in coordinate geometry, enabling students to precisely locate the center between two points. This collection of examples aids in teaching the topic by providing clear visual representations alongside detailed calculations. Students can observe how the formula is consistently applied across different scenarios, including points in different quadrants and with varying positive and negative coordinates, reinforcing its universal applicability in coordinate geometry.
Presenting multiple worked-out examples is essential for students to fully comprehend the midpoint formula. By examining the formula's application to points with different coordinates, in various quadrants, and with positive and negative values, students develop a more robust understanding. This repetition helps cement the process and builds confidence in applying the formula to diverse situations they may encounter in both academic and real-world contexts.
Teacher's Script: Now, let's tackle this interesting example together. We have two points on our coordinate plane, one on the y-axis in Quadrant I and one in Quadrant IV. Our goal is to find the point exactly in the middle. Remember, the midpoint formula helps us find the average of both the x-coordinates and the y-coordinates, even when dealing with points in different quadrants. As we work through this, consider how this method might be useful in real-world applications, such as finding the center point of a diagonal line crossing through different quadrants in a graph representing data with both positive and negative values, like temperature changes or profit/loss scenarios!
For a complete collection of math examples related to the Midpoint Formula click on this link: Math Examples: Midpoint Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.B.6 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Geometric Concepts • Midpoint Formula |
| Copyright Year | 2013 |
| Keywords | midpoint formula, coordinates |