Display Title
Math Example--Coordinate Geometry--The Midpoint Formula: Example 9
Display Title
Math Example--Coordinate Geometry--The Midpoint Formula: Example 9
Topic
Coordinate Geometry
Description
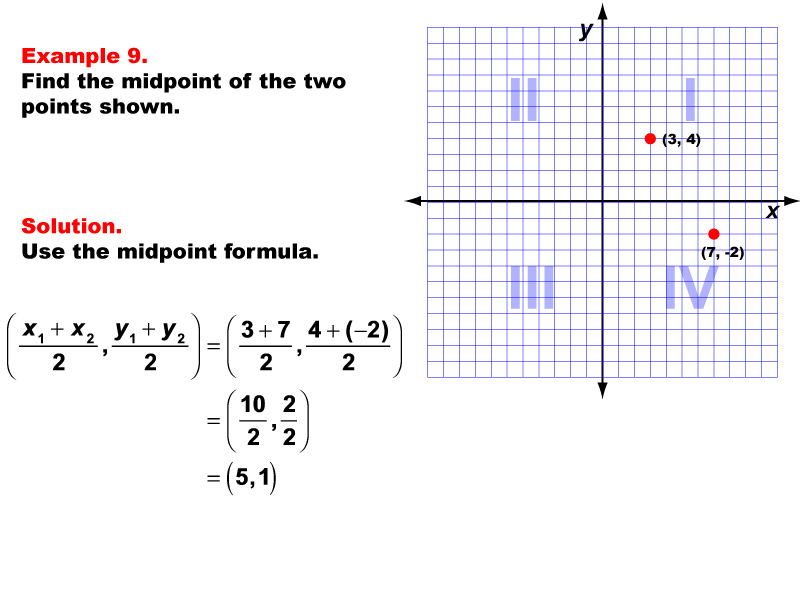
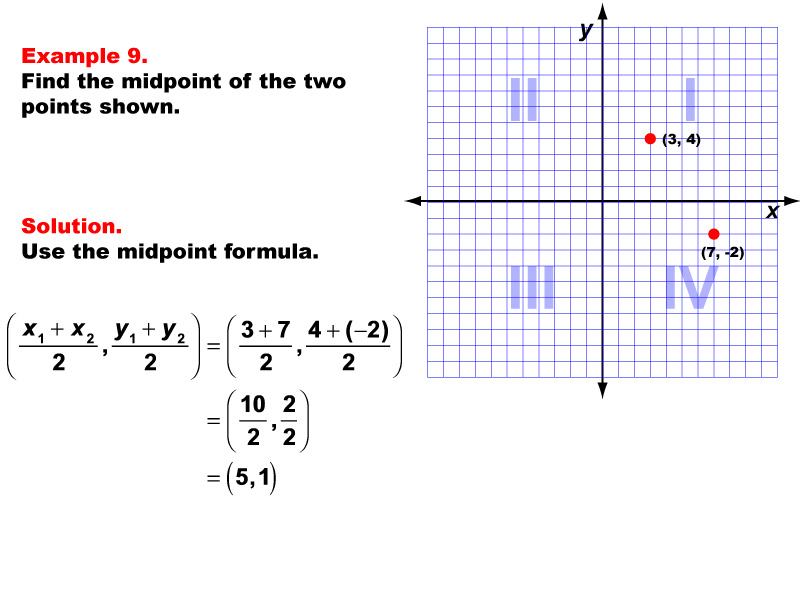
This example demonstrates the application of the midpoint formula to find the center point between (3, 4) and (7, -2) on a coordinate plane. Using the formula ( ( x1 + x2 ) / 2, ( y1 + y2 ) / 2 ), we substitute the given values: ( ( 3 + 7 ) / 2, ( 4 + (-2) ) / 2 ) = ( 10 / 2, 2 / 2 ) = ( 5, 1 ). The resulting midpoint is (5, 1).
The midpoint formula is a crucial concept in coordinate geometry, allowing students to accurately determine the center between two points. This collection of examples aids in teaching the topic by providing clear visual representations alongside step-by-step calculations. Students can observe how the formula is consistently applied across different scenarios, including points in different quadrants and with varying vertical distances, reinforcing its universal applicability in coordinate geometry.
Exposure to multiple worked-out examples is vital for students to fully grasp the midpoint formula concept. By examining the formula's application to points with different coordinates, in various quadrants, and with positive and negative y-values, students develop a more comprehensive understanding. This repetition helps solidify the process and builds confidence in applying the formula to diverse situations they may encounter in both academic and real-world contexts.
Teacher's Script: Let's explore this example together. We have two points on our coordinate plane, one in Quadrant I and one straddling Quadrants I and IV. Our task is to find the point exactly in the middle. Remember, the midpoint formula helps us find the average of both the x-coordinates and the y-coordinates, even when dealing with points that have a significant vertical distance between them. As we work through this, think about how this method could be useful in real-world scenarios, like finding the center of a line segment in a graph representing data with both positive and negative values!
For a complete collection of math examples related to the Midpoint Formula click on this link: Math Examples: Midpoint Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.GPE.B.6 |
|---|---|
| Grade Range | 9 - 12 |
| Curriculum Nodes |
Algebra • Geometric Concepts • Midpoint Formula |
| Copyright Year | 2013 |
| Keywords | midpoint formula, coordinates |