Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 14
Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 14
Topic
Slope Formula
Description
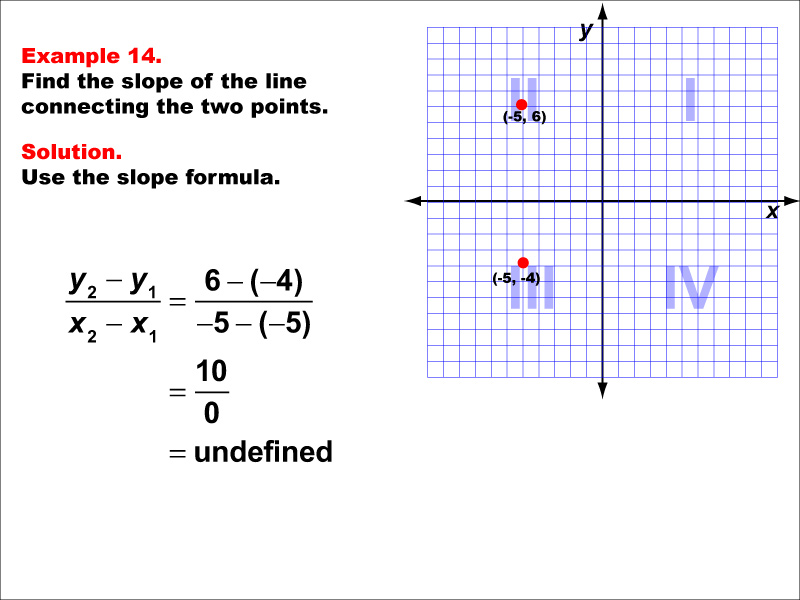
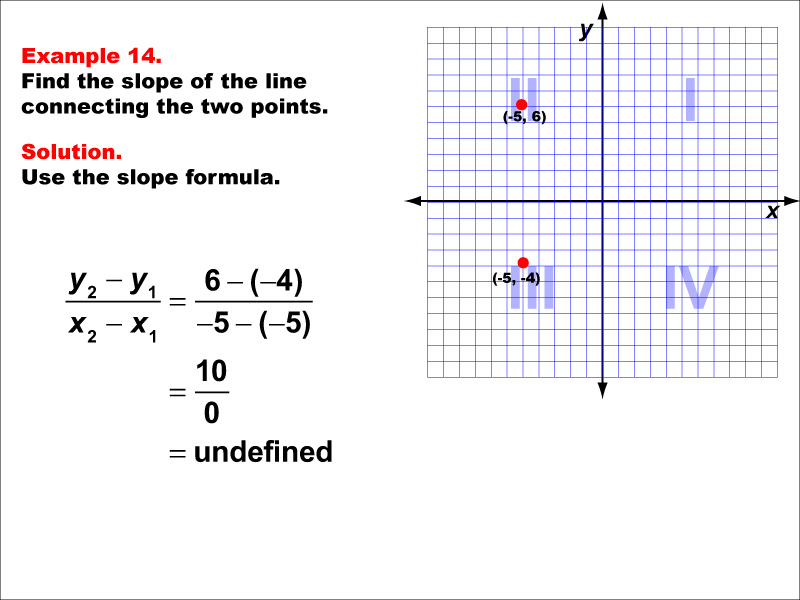
This example illustrates the calculation of slope for a vertical line passing through two points: (-5, 6) and (-5, -4) in Quadrant II of a Cartesian plane. When we apply the slope formula, we find that the slope is (6 - (-4)) / (-5 - (-5)) = 10 / 0, which is undefined.
The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is vertical, resulting in an undefined slope.
Providing multiple examples like this allows students to encounter various scenarios, including special cases. This helps reinforce the concept and improves their ability to interpret slopes in different situations, particularly when dealing with vertical lines.
Teacher's Script: Take a close look at this example. Notice that the x-coordinates of both points are the same, resulting in a vertical line. When we try to calculate the slope, we end up dividing by zero, which is undefined in mathematics. This is why we say that vertical lines have an undefined slope. How does this compare to horizontal lines? Can you think of real-world examples where we might encounter vertical lines? How would you describe the steepness of a vertical line without using the term 'slope'?
For a complete collection of math examples related to Slope Formula click on this link: Math Examples: Slope Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.2.D |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope |
| Copyright Year | 2013 |
| Keywords | slope, rise over run, slope formula |