Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 2
Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 2
Topic
Slope Formula
Description
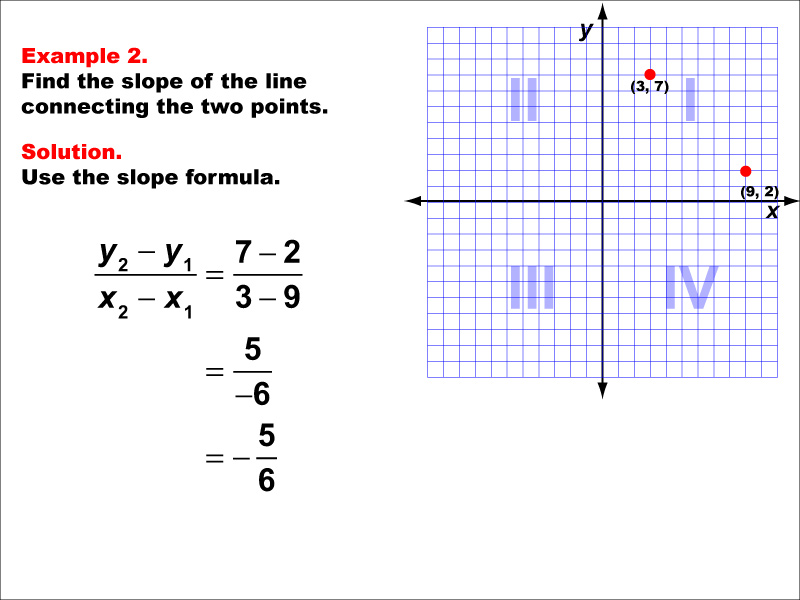
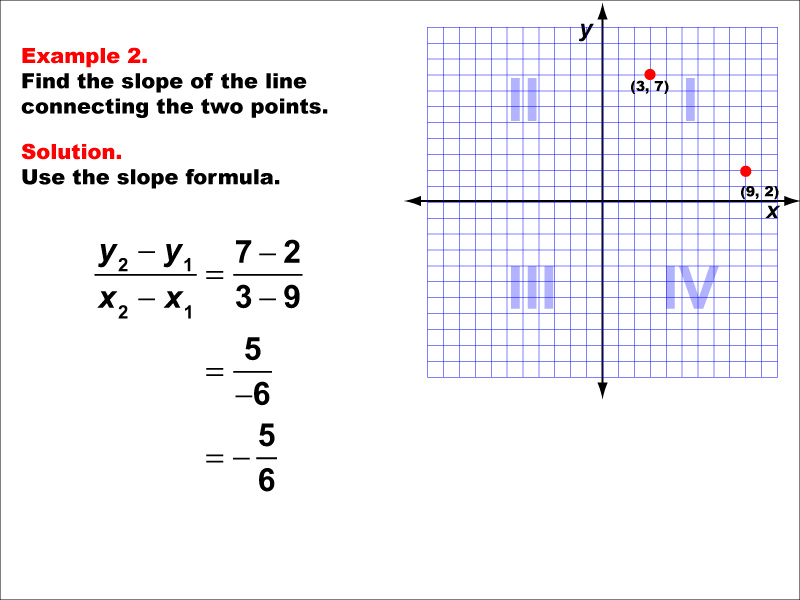
This example illustrates the calculation of slope between two points (3, 7) and (9, 2) on a coordinate grid. The slope formula is applied to find that the slope is (7 - 2) / (3 - 9) = 5 / -6 = -5 / 6.
Understanding the slope formula is crucial in coordinate geometry as it helps describe the steepness and direction of a line. This concept is widely used in various mathematical applications and real-world scenarios.
Providing multiple examples like this one allows students to see how the slope formula can be applied in different situations. This repetition helps reinforce the concept and improves students' ability to calculate slopes accurately across various problems.
Teacher's Script: Take a close look at this example. Notice how the slope is negative, indicating that the line is decreasing as we move from left to right. Remember, the slope tells us how much the line rises or falls for each unit it moves horizontally. In this case, for every 6 units we move to the right, the line falls by 5 units.
For a complete collection of math examples related to Slope Formula click on this link: Math Examples: Slope Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.2.D |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope |
| Copyright Year | 2013 |
| Keywords | slope, rise over run, slope formula |