Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 20
Display Title
Math Example--Coordinate Geometry--Slope Formula: Example 20
Topic
Slope Formula
Description
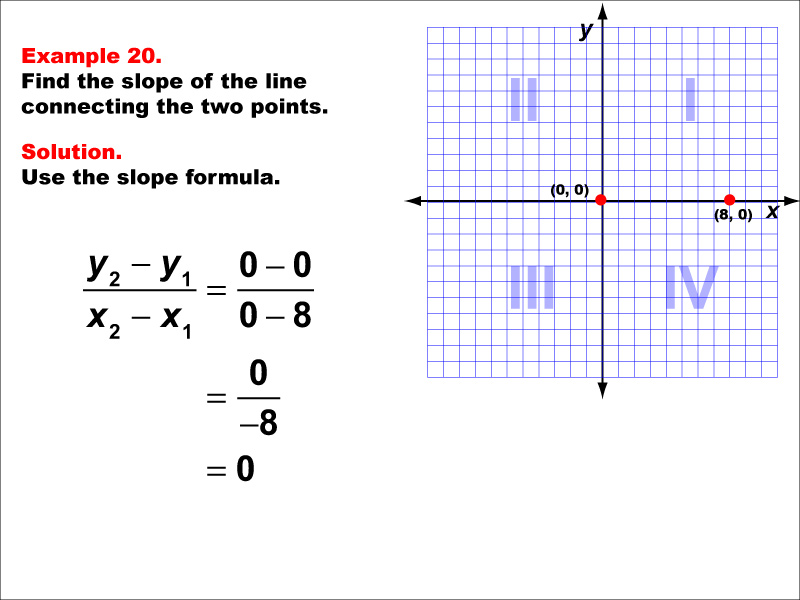
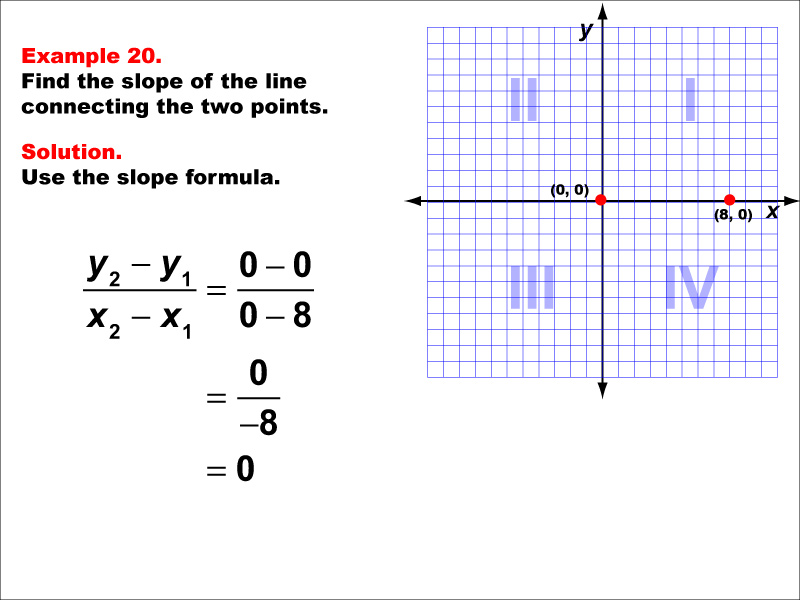
This example demonstrates the calculation of slope for a horizontal line connecting points (0, 0) and (8, 0) on a Cartesian plane. When we apply the slope formula, we find that the slope is (0 - 0) / (8 - 0) = 0 / 8 = 0.
The slope formula is a key concept in coordinate geometry, helping us understand the steepness and direction of lines. This particular example highlights a special case where the line is horizontal and lies on the x-axis, resulting in a slope of zero.
By providing multiple examples like this, students can see how the slope formula applies in various scenarios, including special cases. This helps reinforce the concept and improves their ability to interpret slopes in different situations, particularly when dealing with horizontal lines.
Teacher's Script: Let's examine this example carefully. Notice that both points lie on the x-axis, resulting in a horizontal line. When we calculate the slope, we get zero. This means that for any horizontal movement, there is no change in height. How does this compare to the other horizontal line we saw earlier? Can you think of real-world examples where we might encounter lines that lie exactly on the x-axis? How would you describe the difference between this line and a line with a very small, but non-zero slope?
For a complete collection of math examples related to Slope Formula click on this link: Math Examples: Slope Formula Collection.
| Common Core Standards | CCSS.MATH.CONTENT.8.EE.B.5, CCSS.MATH.CONTENT.7.RP.A.2.D |
|---|---|
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Slope |
| Copyright Year | 2013 |
| Keywords | slope, rise over run, slope formula |